
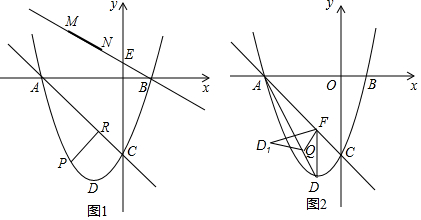
���� ��1���ֱ���x=0��y=0���ɵ�A��B��C�������꣬���ô���ϵ������ֱ��AC�Ľ���ʽΪy=kx+b��ת��Ϊ�ⷽ���鼴�ɣ�
��2����ͼ1�У���P��m��m2+2m-3���������⣬��PR���ʱ����ACP���������ı���APCO����������ΪS�ı���APCO=S��AOP+S��POC-S��AOC=$\frac{1}{2}$•3•��-m2-2m+3��+$\frac{1}{2}$•3•��-m��-$\frac{1}{2}$•3•3=-$\frac{3}{2}$m2-$\frac{9}{2}$m=-$\frac{3}{2}$��m+$\frac{3}{2}$��2+$\frac{27}{8}$�����Ե�m=-$\frac{3}{2}$ʱ���ı���APCO��������PR����ɵ�P��-$\frac{3}{2}$��-$\frac{15}{4}$��������P��BE����ƽ��$\sqrt{5}$����λ�õ�G��-$\frac{7}{2}$��-$\frac{11}{4}$��������A����ֱ��BE�ĶԳƵ�K������GK��BE��M����ʱ�ı���APNM�����С����취�����M�����꼴�ɽ�����⣮
��3���������������ۼ��ɢ���ͼ2�У���FD1��ADʱ���ص�������Rt��FKQ������ͼ3�У���FQ��ADʱ���ص�������Rt��FQD1������ͼ4�У���QD1��ACʱ���ص�������Rt��QMF���ֱ����AQ���ɣ�
��� �⣺��1������������y=x2+2x-3����y=0����x2+2x-3=0�����x=-3��1��
��A��-3��0����B��1��0����
��x=0����y=-3��
��C��0��-3����
��������y=x2+2x-3=��x+1��2-4��
�ඥ��D����Ϊ��-1��-4����
��ֱ��AC�Ľ���ʽΪy=kx+b������$\left\{\begin{array}{l}{b=-3}\\{-3k+b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-1}\\{b=-3}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=-x-3����D���꣨-1��-4����
��2����ͼ1�У���P��m��m2+2m-3����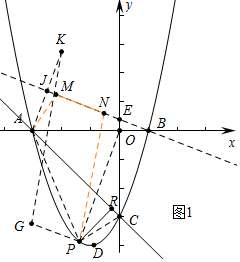
�����⣬��PR���ʱ����ACP���������ı���APCO��������
��S�ı���APCO=S��AOP+S��POC-S��AOC=$\frac{1}{2}$•3•��-m2-2m+3��+$\frac{1}{2}$•3•��-m��-$\frac{1}{2}$•3•3=-$\frac{3}{2}$m2-$\frac{9}{2}$m=-$\frac{3}{2}$��m+$\frac{3}{2}$��2+$\frac{27}{8}$��
�൱m=-$\frac{3}{2}$ʱ���ı���APCO��������PR���
��P��-$\frac{3}{2}$��-$\frac{15}{4}$����
����P��BE����ƽ��$\sqrt{5}$����λ�õ�G��-$\frac{7}{2}$��-$\frac{11}{4}$��������A����ֱ��BE�ĶԳƵ�K������GK��BE��M����ʱ�ı���APNM�����С��
��ֱ��BE�Ľ���ʽΪy=-$\frac{1}{2}$x+$\frac{1}{2}$��ֱ��AK�Ľ���ʽΪy=2x+6��
��$\left\{\begin{array}{l}{y=2x+6}\\{y=-\frac{1}{2}x+\frac{1}{2}}\end{array}\right.$���$\left\{\begin{array}{l}{x=-\frac{11}{5}}\\{y=\frac{8}{5}}\end{array}\right.$��
��J��-$\frac{11}{5}$��$\frac{8}{5}$����
��AJ=JK��
��k��-$\frac{7}{5}$��$\frac{16}{5}$����
��ֱ��KG�Ľ���ʽΪy=$\frac{17}{6}$x+$\frac{43}{6}$��
��$\left\{\begin{array}{l}{y=\frac{17}{6}x+\frac{43}{6}}\\{y=-\frac{1}{2}x+\frac{1}{2}}\end{array}\right.$���$\left\{\begin{array}{l}{x=-2}\\{y=\frac{3}{2}}\end{array}\right.$��
��M��-2��$\frac{3}{2}$��������M����ƽ��1����λ������ƽ��2����λ�õ�N��
��N��0��$\frac{1}{2}$����
��3�����ڣ�
����ͼ2�У���FD1��ADʱ���ص�������Rt��FKQ����QM��DF��M��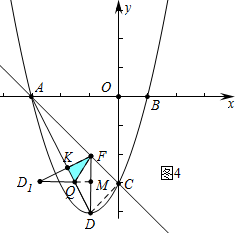
�������֪F��-1��-2����DF=2��AF=2$\sqrt{2}$��AC=3$\sqrt{2}$��AD=2$\sqrt{5}$
�ɡ�AKF�ס�ACD����$\frac{AF}{AD}$=$\frac{FK}{CD}$=$\frac{AK}{AC}$��
��$\frac{2\sqrt{2}}{2\sqrt{5}}$=$\frac{FK}{\sqrt{2}}$=$\frac{AK}{3\sqrt{2}}$
��FK=$\frac{2\sqrt{5}}{5}$��AK=$\frac{6\sqrt{5}}{5}$��
��DK=$\sqrt{{2}^{2}-��\frac{2\sqrt{5}}{5}��^{2}}$=$\frac{4\sqrt{5}}{5}$����QK=QM=x��
��Rt��QMD��x2+��2-$\frac{2\sqrt{5}}{5}$��2=��$\frac{4\sqrt{5}}{5}$-x��2��
��x=1-$\frac{\sqrt{5}}{5}$��
��AQ=AK+KQ=1+$\sqrt{5}$
����ͼ3�У���FQ��ADʱ���ص�������Rt��FQD1����ʱAQ=$\frac{6\sqrt{5}}{5}$��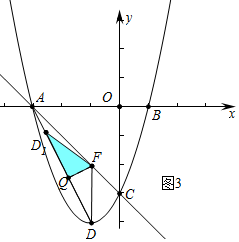
����ͼ4�У���QD1��ACʱ���ص�������Rt��QMF��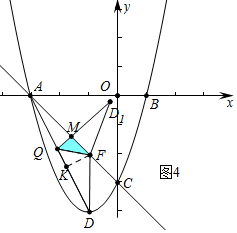
��QM=QK=x����Rt��AQM��x2+��2$\sqrt{2}$-$\frac{2\sqrt{5}}{5}$��2=��$\frac{6\sqrt{5}}{5}$-x��2��
��x=$\frac{2\sqrt{2}}{3}$-$\frac{2\sqrt{5}}{15}$��
��AQ=AK-QK=$\frac{6\sqrt{5}}{5}$-��$\frac{2\sqrt{2}}{3}$-$\frac{2\sqrt{5}}{15}$��=$\frac{4\sqrt{5}}{3}$-$\frac{2\sqrt{2}}{3}$��
��������������D1FQ���AFQ�ص����ֵ�ͼ����ֱ��������ʱ��AQ�ij�Ϊ1+$\sqrt{5}$��$\frac{6\sqrt{5}}{5}$��$\frac{4\sqrt{5}}{3}$-$\frac{2\sqrt{2}}{3}$��
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á�ֱ�������ε����ʡ�������⡢��Ԫһ�η����顢���ɶ�����֪ʶ������Ĺؼ���ѧ�ṹ��һ�κ������÷����������꣬ѧ�ṹ�����κ��������ֵ���⣬ѧ�����öԳƽ��������⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
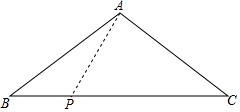 ��ͼ������������ABC�ĵױ߳�Ϊ8cm������Ϊ5cm��һ����P�ڵױ��ϴӵ�B���C��1cm/s���ٶ��ƶ���
��ͼ������������ABC�ĵױ߳�Ϊ8cm������Ϊ5cm��һ����P�ڵױ��ϴӵ�B���C��1cm/s���ٶ��ƶ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
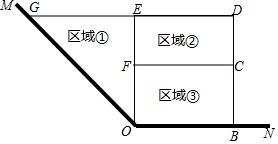 Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ���һ�ǡ�MON����MON=135�㣩������Ϊ�ߣ����ܳ�Ϊ120m��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ������������������Ϊֱ�������Σ�����ڢ�Ϊ���Σ������ı���OBDGΪֱ�����Σ�
Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ���һ�ǡ�MON����MON=135�㣩������Ϊ�ߣ����ܳ�Ϊ120m��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ������������������Ϊֱ�������Σ�����ڢ�Ϊ���Σ������ı���OBDGΪֱ�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����B����C��ƽ�����ཻ��F������F��DE��BC����AB��D����AC��E����ô���н��ۣ��١�BDF����CEF���ǵ��������Σ� ��DE=BD+CE���ۡ�ADE���ܳ�ΪAB+AC����BD=CE��������ȷ���ǣ�������
��ͼ����B����C��ƽ�����ཻ��F������F��DE��BC����AB��D����AC��E����ô���н��ۣ��١�BDF����CEF���ǵ��������Σ� ��DE=BD+CE���ۡ�ADE���ܳ�ΪAB+AC����BD=CE��������ȷ���ǣ�������| A�� | �ۢ� | B�� | �٢� | C�� | �٢ڢ� | D�� | �ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
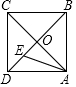 ��ͼ��������ABCD�ı߳�Ϊa��AC��BD���ڵ�O��EΪOD�е㣬����P�ӵ�O����������O��E��A��B��O��·���˶����ص���Oʱ�˶�ֹͣ�����P�˶���·�̳�Ϊx��AP��Ϊy����y����x�ĺ���ͼ������� ��������
��ͼ��������ABCD�ı߳�Ϊa��AC��BD���ڵ�O��EΪOD�е㣬����P�ӵ�O����������O��E��A��B��O��·���˶����ص���Oʱ�˶�ֹͣ�����P�˶���·�̳�Ϊx��AP��Ϊy����y����x�ĺ���ͼ������� ��������| A�� | 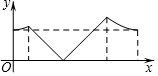 | B�� | 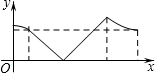 | ||
| C�� | 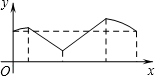 | D�� | 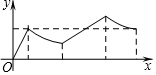 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com