
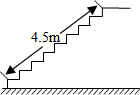
 某中学要修建一座图书楼,为改善安全性能,把楼梯的倾斜角由原来设计的45°改为30°.已知原来设计的楼梯长为4.5m,在楼梯高度不变的情况下,调整后的楼梯多占地面$\frac{9\sqrt{6}-9\sqrt{2}}{4}$m.
某中学要修建一座图书楼,为改善安全性能,把楼梯的倾斜角由原来设计的45°改为30°.已知原来设计的楼梯长为4.5m,在楼梯高度不变的情况下,调整后的楼梯多占地面$\frac{9\sqrt{6}-9\sqrt{2}}{4}$m. 分析 由题可知45°、30°的角在两个直角三角形中,且对边相等,只需利用正切函数求出邻边后,求它们的差即可.
解答 解:如图,
设楼梯的高为AC,原楼梯所占的地面长为BC,调整后楼梯多占的长为BD,
则在Rt△ABC,AC=ABsin45°=4.5sin45°=$\frac{9\sqrt{2}}{4}$m,BC=ABcos45°=4.5cos45°=$\frac{9\sqrt{2}}{4}$m.
在Rt△ACD中,DC=AC÷tan30°=$\frac{9\sqrt{2}}{4}$×$\sqrt{3}$=$\frac{9\sqrt{6}}{4}$m.
∴DB=DC-BC=$\frac{9\sqrt{6}}{4}$-$\frac{9\sqrt{2}}{4}$=$\frac{9\sqrt{6}-9\sqrt{2}}{4}$m.
∴调整后的楼梯多占地面$\frac{9\sqrt{6}-9\sqrt{2}}{4}$m.
故答案为:$\frac{9\sqrt{6}-9\sqrt{2}}{4}$.
点评 本题主要考查了坡度坡角问题,解题的关键利用三角函数得到修改前的水平距离和修改后的水平距离.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
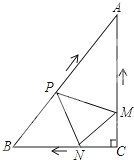 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t≤2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t≤2.5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.3×102千米 | B. | 6.3×103千米 | C. | 0.63×104千米 | D. | 630×10千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
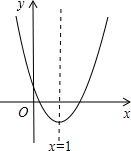 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0.其中正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0.其中正确的是( )| A. | ①③ | B. | ② | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
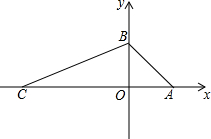 如图,在平面直角坐标系中,O为坐标原点,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P是线段CA上一动点.
如图,在平面直角坐标系中,O为坐标原点,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P是线段CA上一动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com