
【题目】下列定理中,逆命题是假命题的是( )
A.等腰三角形的底角相等;
B.全等三角形的对应角相等;
C.直角三角形斜边上的中线等于斜边的一半;
D.线段垂直平分线上的任意一点到这条线段两个端点的距离相等。
【答案】B
【解析】
先分别写出各选项对应的逆命题,根据等腰三角形的判定定理、全等三角形的判定定理、直角三角形的判定定理和垂直平分线的判定定理逐一判断即可.
A选项的逆命题为:有两个角相等的三角形是等腰三角形,根据等角对等边,此逆命题正确,故A不符合题意;
B选项的逆命题为:对应角相等的两个三角形全等,对应角相等的两三角形不一定全等(如相似),此逆命题错误,故B符合题意;
C选项的逆命题为:如果一个三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形,如下图所示,CD为△ABC的中线,且CD=![]() AB
AB
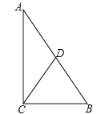
可得:DC=DA=DB
∴∠A=∠DCA,∠B=∠DCB
∴∠A+∠B=∠DCA+∠DCB=∠ACB
∵∠A+∠B+∠ACB =180°
∴∠ACB =90°
∴△ACB是直角三角形,此逆命题正确
故C不符合题意;
D选项的逆命题为:到线段两个端点距离相等的点在这条线段的垂直平分线上,根据垂直平分线的判定定理,此逆命题正确,故D不符合题意.
故选B.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】(1).如图①,已知AB∥CD,求证:∠A+∠C=∠E
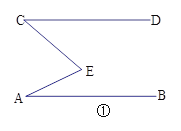
(2)直接写出当点E的位置分别如图②、图③、图④的情形时∠A、∠C、∠AEC之间的关系.
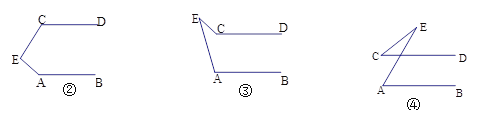
②中∠C、∠A、∠AEC之间的关系为 ;
③中∠C、∠A、∠AEC之间的关系为 ;
④中∠C、∠A、∠AEC之间的关系为 ;
(3)在(2)中的3中情形中任选一种进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=![]() ,BC=8.
,BC=8.
(1)动手操作:
利用尺规作以AC为直径的圆O,并标圆O与AB的交点D,与BC的交点E,连接DE、CE(保留作图痕迹,不写作法)
(2)综合应用:
在你所作的图中,①求证:DE=CE;②求DC的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图:在△ABC中,∠B=90°,∠A=30°,BC=5cm,等腰Rt△DEF中,∠FDE=![]() ,DE=3cm。动点D、E始终在边AB上,当点D从A点沿AC方向移动。
,DE=3cm。动点D、E始终在边AB上,当点D从A点沿AC方向移动。
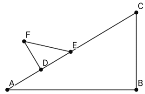
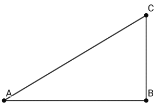
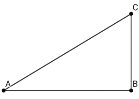
(1)在Rt△DEF沿AC方向移动的过程中,F,C两点之间的距离逐渐_______。(填“不变“变大”或“变小”)
(2)当F、C连线与AB平行时,求AD的长。
(3)以线段AD、FC、BC的长度为三边长的三角形是直角三角形时,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=![]() (k≠0)的图象过点C,则该反比例函数的表达式为_______.
(k≠0)的图象过点C,则该反比例函数的表达式为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周的某一天,小王全家上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离![]() (千米)与小汽车离家后时间
(千米)与小汽车离家后时间![]() (时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:

(1)“番茄农庄”离家________千米;
(2)小王全家在“番茄农庄”游玩了________小时;
(3)去时小汽车的平均速度是________千米/小时;
(4)回家时小汽车的平均速度是________千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,线段
,线段![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始绕着点
开始绕着点![]() 以
以![]() 的速度顺时针旋转一周回到点
的速度顺时针旋转一周回到点![]() 后停止,点
后停止,点![]() 同时出发沿射线
同时出发沿射线![]() 自
自![]() 点向
点向![]() 点运动,若点
点运动,若点![]() 、
、![]() 两点能恰好相遇,则点
两点能恰好相遇,则点![]() 运动的速度为________
运动的速度为________![]() ;
;

![]() 将一副三角板中的两块直角三角尺的直角顶点
将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起(其中,
按如图方式叠放在一起(其中,![]() ,
,![]() ,
,![]() ;
;![]() ).将三角尺
).将三角尺![]() 固定,另一三角尺
固定,另一三角尺![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 转动,转动速度与
转动,转动速度与![]() 问中
问中![]() 点速度相同,当
点速度相同,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 有可能的值及对应转动的时间;若不存在,请说明理由.
有可能的值及对应转动的时间;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com