
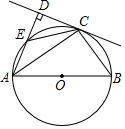
 如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.分析 (1)连接OC,利用切线的性质和已知条件推知OC∥AD,根据平行线的性质和等角对等边证得结论;
(2)AE=AD-ED,通过相似三角形△ADC∽△ACB的对应边成比例求得AD=4,DC=2.在直角△DCE中,由勾股定理得到DE=$\sqrt{E{C}^{2}-D{C}^{2}}$=1,故AE=AD-ED=3.
解答  (1)证明:连接OC,
(1)证明:连接OC,
∵CD是⊙O的切线,
∴OC⊥CD.
∵AD⊥CD,
∴OC∥AD,
∴∠1=∠3.
又OA=OC,
∴∠2=∠3,
∴∠1=∠2,
∴CE=CB;
(2)解:∵AB是直径,
∴∠ACB=90°,
∵AC=2$\sqrt{5}$,CB=CE=$\sqrt{5}$,
∴AB=$\sqrt{A{C}^{2}+C{B}^{2}}$=$\sqrt{(2\sqrt{5})^{2}+(\sqrt{5})^{2}}$=5.
∵∠ADC=∠ACB=90°,∠1=∠2,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$=$\frac{DC}{CB}$,即$\frac{AD}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$=$\frac{DC}{\sqrt{5}}$,
∴AD=4,DC=2.
在直角△DCE中,DE=$\sqrt{E{C}^{2}-D{C}^{2}}$=1,
∴AE=AD-ED=4-1=3.
点评 本题考查了切线的性质,勾股定理,相似三角形的判定与性质,解题时,注意辅助线的作法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.
如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.
某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
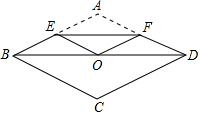
 如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )| A. | (20$\sqrt{3}$-20)cm | B. | (40$\sqrt{3}$-40)cm | C. | (60-30$\sqrt{3}$)cm | D. | (60$\sqrt{3}$-60)cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,则△ABC中,∠BAC=100°,AB=AC=4,以点B为圆心,BA长为半径作圆弧,交BC于点D,则$\widehat{AD}$的长为$\frac{8π}{9}$.(结果保留π)
如图,则△ABC中,∠BAC=100°,AB=AC=4,以点B为圆心,BA长为半径作圆弧,交BC于点D,则$\widehat{AD}$的长为$\frac{8π}{9}$.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )
如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )| A. | 120° | B. | 100° | C. | 60° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com