
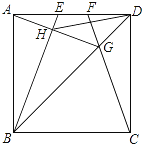
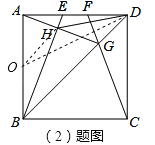
【题目】如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2 ![]() ﹣2.
﹣2.
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
解:∵四边形ABCD是正方形,∴AB=CD,∠BAD=∠ADC=90°,∠ADB=∠CDB=45°.在△ABE和△DCF中,∵AB=CD,∠BAD=∠ADC,AE=DF,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF.在△ADG和△CDG中,∵AD=CD,∠ADB=∠CDB,DG=DG,∴△ADG≌△CDG(SAS),∴∠DAG=∠DCF,∴∠ABE=∠DAG.∵∠DAG+∠BAH=90°,∴∠ABE+∠BAH=90°,∴∠AHB=90°,∴AG⊥BE,故③正确.
同法可证:△AGB≌△CGB.∵DF∥CB,∴△CBG∽△FDG,∴△ABG∽△FDG,故①正确.
∵S△HDG:S△HBG=DG:BG=DF:BC=DF:CD=tan∠FCD.又∵∠DAG=∠FCD,∴S△HDG:S△HBG=tan∠FCD,tan∠DAG,故④正确.
取AB的中点O,连接OD、OH,∵正方形的边长为4,∴AO=OH=![]() ×4=2,由勾股定理得,OD=
×4=2,由勾股定理得,OD=![]() =
=![]() ,由三角形的三边关系得,O、D、H三点共线时,DH最小,DH最小=
,由三角形的三边关系得,O、D、H三点共线时,DH最小,DH最小=![]() .故⑤正确.
.故⑤正确.
无法证明DH平分∠EHG,故②错误,故①③④⑤正确,故选C.


科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生体质情况,从各年级学生中随机抽取部分学生进行体能测试.
每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制 成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
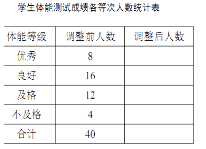
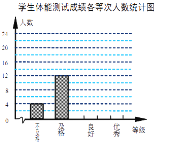
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台州某校七(1)班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
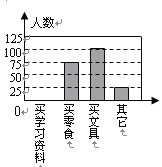
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
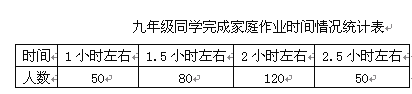
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?

![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
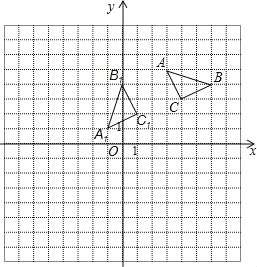
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
(1)在图中标示出旋转中心P,并写出它的坐标;
(2)以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2,在图中画出△A2B2C2,并写出C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
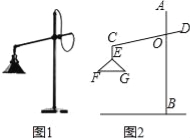
【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为8元/千克的水果,经试销发现,销量y(千克)与销售单价x(元)符合一次函数y=kx+b,且当x=10时,y=300;当x=13时,y=150.
(1)求y(千克)与x(元)(x>8)的函数关系式;
(2)设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,△ABC各顶点的坐标分别是A(﹣2,4),B(﹣4,3),C(﹣1,1).将△ABC向右平移5个单位长度,再向下平移4个单位长度得到△A′B′C′.
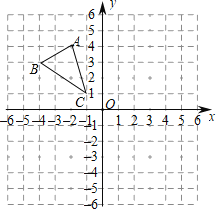
(1)请作出平移后的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)如果将△A′B′C′看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com