
| 厂家 | 超过标准质量的部分 | |||||
| 甲 | -3 | 0 | 0 | 1 | 2 | 0 |
| 乙 | -2 | 1 | -1 | 0 | 1 | 1 |
分析 (1)求出记录的质量的和,再加上标准质量,计算即可得解;
(2)以标准质量为基准,根据方差的定义计算两公司的方差,方差小的质量比较稳定.
解答 解:(1)甲厂抽样检测的皮具总质量为500×6+(-3+0+0+1+2+0)=3000(克),
乙厂抽样检测的皮具总质量为500×6+(-2+1-1+0+1+1)=3000(克);
(2)∵$\overline{{x}_{甲}}$=$\frac{1}{6}$×(-3+0+0+1+2+0)=0,
∴${{S}_{甲}}^{2}$=$\frac{1}{6}$×[(-3-0)2+(0-0)2×3+(1-0)2+(2-0)2]≈2.33,
∵$\overline{{x}_{乙}}$=$\frac{1}{6}$×(-2+1-1+0+1+1)=0,
∴${{S}_{乙}}^{2}$=$\frac{1}{6}$×[(-2-0)2+3×(1-0)2+(-1-0)2+(0-0)2]≈1.33,
∵${{S}_{乙}}^{2}$<${{S}_{甲}}^{2}$,
∴乙公司生产皮具的质量比较稳定.
点评 本题主要考查方差,用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果叫方差.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
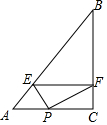 如图,△ABC中,∠C=90°,BC=4,AC=3,P是边AC上的一动点,PE⊥AB于点E,EF⊥BC于点F.设AP=x,则能使以点P、C、F为顶点的三角形与以A、P、E为顶点的三角形相似的x=$\frac{75}{34}$或$\frac{75}{41}$.
如图,△ABC中,∠C=90°,BC=4,AC=3,P是边AC上的一动点,PE⊥AB于点E,EF⊥BC于点F.设AP=x,则能使以点P、C、F为顶点的三角形与以A、P、E为顶点的三角形相似的x=$\frac{75}{34}$或$\frac{75}{41}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax | B. | $\frac{3}{4}$ax | C. | -$\frac{3}{4}$ax | D. | -$\frac{1}{4}$ax |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5700000=57×106 | |
| B. | 0.0158(用四舍五入法精确到0.001)≈0.015 | |
| C. | 0.0000275=2.75×10-6 | |
| D. | 1.967(用四舍五入法精确到十分位)≈2.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

小明发现四边形ABCD的一组领边AD=CD,这就为旋转作了铺垫.于是,小明同学有如下思考过程: 第一步:将△ADE绕点D逆时针旋转90°; 第二步:利用∠A与∠DCB互补, 证明F、C、B三点共线, 从而得到正方形DEBF; 进而求得四边形ABCD的面积. 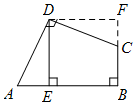 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 7 | D. | -7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com