
【题目】如图,已知在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与一次函数
与一次函数![]() 的图象相交于点
的图象相交于点![]() ,过点
,过点![]() 作
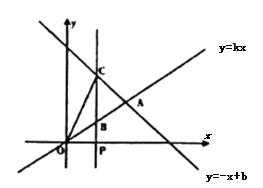
作![]() 轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
(1)求这两个函数解析式.
(2)求![]() 的面积.
的面积.
(3)在坐标轴上存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形,请直接写出
为腰的等腰三角形,请直接写出![]() 点的坐标。
点的坐标。
【答案】(1)正比例函数解析式为![]() ;一次函数解析式为
;一次函数解析式为![]() ;(2)
;(2)![]() ;(3)M(10,0)或M(-10,0)或M(0,10)或M(0,-10)或(16,0)或(0,12)
;(3)M(10,0)或M(-10,0)或M(0,10)或M(0,-10)或(16,0)或(0,12)
【解析】
(1)将A点坐标分别代入正比例函数和一次函数解析式,即可得解;
(2)首先根据题意求出点B和C的坐标,即可得出BC,进而得出△OBC的面积;
(3)首先根据点A坐标求出OA,即可得出腰长,然后分情况讨论:x轴和y轴,即可得解.
(1)根据题意,将![]() 分别代入正比例函数和一次函数解析式,得
分别代入正比例函数和一次函数解析式,得
![]() ,解得
,解得![]()
正比例函数解析式为![]()
![]() ,解得
,解得![]()
一次函数解析式为![]()
(2)根据题意,得
![]() ,
,![]()
∴![]()
∴![]()
(3)根据题意,得OA=10
当点M在x轴上时,其坐标为M(10,0)或M(-10,0)或(16,0);
当点M在y轴上时,其坐标为M(0,10)或M(0,-10)或(0,12);
故点M的坐标为(10,0)或(-10,0)或(0,10)或(0,-10)或(16,0)或(0,12)


科目:初中数学 来源: 题型:
【题目】观察:下列图形是由边长为1的小正方形构成的,第1个图形由2个小正方形构成,周长为8;第2个图形是由5个边长为1的小正方形构成,周长为12;![]() 推测:第
推测:第![]() 个图形由________个小正方形构成,周长为_______.
个图形由________个小正方形构成,周长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图形是由边长为l的正方形按照某种规律排列而组成的.
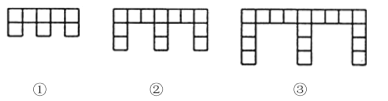
(1)观察图形,填写下表:

(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业在“蜀南竹海”收购毛竹,直接销售,每吨可获利100元,进行粗加工,每天可加工8吨,每吨可获利800元;如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元.由于受条件限制,每天只能采用一种方式加工,要求将在一月内(30天)将这批毛竹93吨全部销售.为此企业厂长召集职工开会,让职工讨论如何加工销售更合算.
甲说:将毛竹全部进行粗加工后销售;
乙说:30天都进行精加工,未加工的毛竹直接销售;
丙说:30天中可用几天粗加工,再用几天精加工后销售;
请问厂长应采用哪位说的方案做,获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为10,
表示的数为10,![]() 是数轴上位于点
是数轴上位于点![]() 左侧一点,且
左侧一点,且![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为
出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
(1)数轴上的点![]() 表示的数是___________,点
表示的数是___________,点![]() 表示的数是__________(用含
表示的数是__________(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,在点
的中点,在点![]() 运动的过程中,线段
运动的过程中,线段![]() 的长度是__________;
的长度是__________;
(3)动点![]() 从点
从点![]() 处出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点
处出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点![]() 同时发出,问点
同时发出,问点![]() 运动多少秒时与点
运动多少秒时与点![]() 相距4个单位长度?
相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
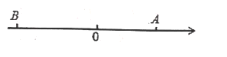
【题目】如图,数轴上的三点A、B、C分别表示有理数a、b、c,且|a|>|c|>|b|.
(1)化简|a+c|﹣2|c﹣b|;
(2)若b的倒数是它本身,且AB:BO:OC=6:2:3,求(1)中代数式的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的 日销售量(件)与时间(天)的关系如下表:
时间(天) | 1 | 3 | 6 | 10 | 36 | … |
日销售量(件) | 94 | 90 | 84 | 76 | 24 | … |
未来40天内,前20天每天的价格y1(元/件)与t时间(天)的函数关系式为:y1=![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—
t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—![]() t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
(1)认真分析上表中的数量关系,利用学过的一次函数、二次函数 、反比例函数的知识确定一个满足这些数据之间的函数关系式;
(2)请预测未来40天中那一天的销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程,公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com