
【题目】一张如图1的长方形铁皮,四个角都剪去边长为30厘米的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是4a(cm),宽是3a(cm),这个无盖铁盒各个面的面积之和称为铁盒的全面积.
(1)请用a的代数式表示图1中原长方形铁皮的面积;
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可漆的面积为![]() (cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(3)铁盒的底面积是全面积的几分之几(用a的代数式表示)?若铁盒的底面积是全面积的![]() , 求a的值;
, 求a的值;
(4)是否存在一个正整数a,使得铁盒的全面积是底面积的正整数倍?若存在,请求出这个a,若不存在,请说明理由.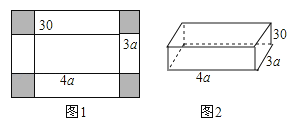
【答案】解:(1)原铁皮的面积是(4a+60)(3a+60)=12a2+420a+3600;
(2)油漆这个铁盒的表面积是:12a2+2×30×4a+2×30×3a=12a2+420a,
则油漆这个铁盒需要的钱数是:(12a2+420a)÷![]() =(12a2+420a)×
=(12a2+420a)×![]() =600a+21000(元);
=600a+21000(元);
(3)铁盒的底面积是全面积的![]() =
=![]() ;
;
根据题意得:![]() =
=![]() ,
,
解得a=105;
(4)铁盒的全面积是4a×3a+4a×30×2+3a×30×2=12a2+420a,
底面积是12a2 ,
假设存在正整数n,使12a2+420a=n(12a2)
则(n﹣1)a=35,
由题意可知a>![]() >10,
>10,
则a只能为35,n=2.
所以存在铁盒的全面积是底面积的正整数倍,这时a=35.
【解析】(1)根据图形表示出原长方形铁皮的面积即可;
(2)根据原长方形铁皮的面积剪去四个小正方形的面积,求出铁盒的表面积,乘以单价即可得到结果;
(3)用铁盒的底面积除以全面积即可得出底面积是全面积的几分之几,再根据铁盒的底面积是全面积的![]() , 求出a的值即可;
, 求出a的值即可;
(4)假设存在,列出铁盒的全面积和底面积的公式,求整数倍数即可.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】 (2016湖北鄂州第14题)如图,已知直线 ![]() 与x轴、y轴相交于P、Q两点,与y=
与x轴、y轴相交于P、Q两点,与y=![]() 的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+
的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+![]() n=0; ③S△AOP= S△BOQ;④不等式k1x+b>
n=0; ③S△AOP= S△BOQ;④不等式k1x+b>![]() 的解集是x<-2或0<x<1,其中正确的结论的序号是 .
的解集是x<-2或0<x<1,其中正确的结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四边形中,顺次连接各边中点所得的四边形是矩形的是( )
A. 等腰梯形 B. 对角线相等的四边形
C. 平行四边形 D. 对角线互相垂直的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与坐标轴分别交于A(﹣2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,∠A=50°,AB=a,BC=b.则∠B=________,∠C=________,平行四边形ABCD的周长=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,李玉刚同学随爸爸妈妈会老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km/h.设爸爸骑行时间为x(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com