
����Ŀ���Ķ������ǿ����û�Ԫ����ĸߴη��̣��ⷽ��x4��3x2+2��0ʱ������y��x2����ԭ���̿ɱ�Ϊy2+3y+2��0����֮��y1��2��y2��1����y1��2ʱ����x2��2����x1��![]() ��x2����
��x2����![]() ����y2��1ʱ����x2��1����x1��1��x2����1����ԭ���̵Ľ�Ϊx1��
����y2��1ʱ����x2��1����x1��1��x2����1����ԭ���̵Ľ�Ϊx1��![]() ��x2����
��x2����![]() ��x3��1��x4����1�������������������
��x3��1��x4����1�������������������
(1)��֪����(2x2+1)2+2x2��3��0����y��2x2+1����ԭ���̿ɻ�Ϊ_______.
(2)���������ⷨ�ⷽ�̣�(x2��2x)2��3x2+6x��0.
���𰸡�(1)y2+y��4��0��(2)x��2��x=0��x����1��x=3.
��������
��1��������ȫƽ����ʽ�ɰ�ԭʽ��Ϊ(2x2+1)2+2x2+1��4��(2x2+1)2+(2x2+1)��4��Ȼ����y����ʽ���е�2x2+1��
��2��(x2��2x)2��3x2+6x��0��(x2��2x)2��3(x2��2x)��0������x2��2x�������壬��x2��2x��y��ԭ���̼��ɱ���Ϊ����y�ķ��̣��������y��ֵ��������x��ֵ��
��1����y��2x2+1��
��ԭ������ߣ�(2x2+1)2+(2x2+1)��4��y2+y��4��
��ԭ���̿ɻ�Ϊy2+y��4��0��
�ʴ�Ϊ��y2+y��4��0��
��2����x2��2x��y��
��ԭʽ��ߣ�(x2��2x)2��3(x2��2x)��y2��3y��
��y2��3y��0��
��y(y��3)��0��
��y��0��3��
��y��0ʱ����x2��2x��0��
��x(x��2)��0��
��x��2��0��
��y��3ʱ����x2��2x��3��
��x2��2x��3��0��
���x����1��3��
�ʷ��̵Ľ�Ϊx��3��x��2��x��0��x����1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���ϵ�һ�㣬��
���ϵ�һ�㣬��![]() ����
����![]() �ھ���
�ھ���![]() ���ڵ�ƽ���У���
���ڵ�ƽ���У���![]() ����
����![]() �����ֵ��_________��
�����ֵ��_________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�ABC����������Ρ�EDC�й�������C�����С�EDC��120����AB��CE��2![]() ������BE��PΪBE���е㣬����PD��AD
������BE��PΪBE���е㣬����PD��AD
��1��Ϊ���о��߶�AD��PD��������ϵ����ͼ1�еġ�EDC�Ƶ�C��תһ���ʵ��ĽǶȣ�ʹCE��CA�غϣ���ͼ2����ֱ��д��AD��PD��������ϵ��
��2����ͼ1����1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��3����ͼ3������ACD��45�������ACD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�һ�κ���y��x��1��ͼ����x�ᣬy��ֱ��ڵ�A��B���뷴��������y��![]() ��ͼ���ڵ�C��D��CE��x���ڵ�E��
��ͼ���ڵ�C��D��CE��x���ڵ�E��![]() ��
��
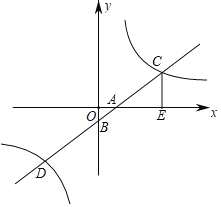
��1�����������ı���ʽ���D�����ꣻ
��2����CEΪ����ECMN����M��һ�κ���y��x��1��ͼ���ϣ����M�ĺ�����Ϊa������MN�뷴��������y��![]() ��ͼ���й�����ʱ����a��ȡֵ��Χ��
��ͼ���й�����ʱ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ��Բ�ĶԳ�����ʱ֪�����ۣ���ֱ���ҵ�ֱ��һ��ƽ�������ң��볢�Խ�����⣺��ͼ����Rt��ACB�У���ACB��90����ԲO����ACB�����Բ����D��ԲO��һ�㣬����D��DE��BC������ΪE����BDƽ�֡�ABE��
��1���ж�ֱ��ED��ԲO��λ�ù�ϵ����˵�����ɣ�
��2����AC��12��BC��5�����߶�BE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
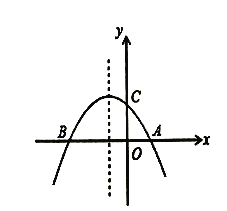
����Ŀ����ͼ,A��B�Ǻ���![]() ͼ���Ϲ���ԭ��ԳƵ�����,��BC//x��,AC//y��,��ABC�������ΪS,��( )
ͼ���Ϲ���ԭ��ԳƵ�����,��BC//x��,AC//y��,��ABC�������ΪS,��( )

A.S=2B.S=4C.S=8D.S=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������ABCD�ı߳�Ϊ4,E��BC�ߵ��е�,��P������AD��,��P��PF��AE��F.
(1)��֤:![]() ;
;
(2)����P������AD���˶�ʱ,��PA=X,�Ƿ����ʵ��x,ʹ��P,F,EΪ�����������Ҳ���ABE����?������,�����x��ֵ;��������,˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
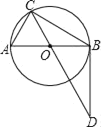
����Ŀ����ͼ��AB����O��ֱ����CΪ��O��һ�㣬��D��CO���ӳ����ϣ�����BD����֪BC��BD��AB��4��
��1����BC��2![]() ����֤��BD����O�����ߣ�
����֤��BD����O�����ߣ�
��2��BC��3����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ����֪������![]() ��
��![]() �ύ��
�ύ��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
![]() ���
���![]() ������;
������;
![]() ��
��![]() �Ǵ��������ϵĵ㣬��
�Ǵ��������ϵĵ㣬��![]() ����Գ����ϵĵ㣬����
����Գ����ϵĵ㣬����![]() Ϊ�����ƽ���ı��ε����;
Ϊ�����ƽ���ı��ε����;
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com