
【题目】如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
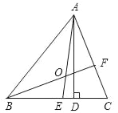
【答案】∠DAE,∠BOA的度数分别是10°,125°
【解析】
根据角平分线的定义可得∠BAE=∠CAE=![]() ∠BAC=30°,在Rt△ADC中可求得∠CAD的度数,再根据∠DAE=∠CAE﹣∠CAD即可得解,根据三角形的内角和可得∠ABC的度数,即可得∠ABO的度数,再在△AOB中利用三角形的内角和为180°即可求得∠BOA的度数.
∠BAC=30°,在Rt△ADC中可求得∠CAD的度数,再根据∠DAE=∠CAE﹣∠CAD即可得解,根据三角形的内角和可得∠ABC的度数,即可得∠ABO的度数,再在△AOB中利用三角形的内角和为180°即可求得∠BOA的度数.
解∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣90°﹣70°=20°,
∵∠BAC=60°,AE是∠BAC的角平分线,
∴∠EAC=∠BAE=30°,
∴∠EAD=∠EAC﹣∠CAD=30°﹣20°=10°,
∠ABC=180°﹣∠BAC﹣∠C=50°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣30°﹣25°=125°.
故∠DAE,∠BOA的度数分别是10°,125°


科目:初中数学 来源: 题型:
【题目】已知:A(2,4),B(1,1),C(5,2).

(1)在如图所示的平面直角坐标系中描出各点,画出三角形ABC;
(2)将三角形ABC向左平移6个单位,再向下平移3个单位,请在图中作出平移后的三角形A1B1C1;
(3)写出三角形各点A1、B1、C1的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需要粉刷一些相同的房间,经调查3名师傅一天粉刷8个房间,还剩40m2刷不完;5名徒弟一天可以粉刷9个房间;每名师傅比徒弟一天多刷30m2的墙面。
(1)求每个房间需要粉刷的面积;
(2)该公司现有36个这样的房间需要粉刷,若只聘请1名师傅和2名徒弟一起粉刷,需要几天完成?
(3)若来该公司应聘的有3名师傅和10名徒弟,每名师傅和每名徒弟每天的工资分别是240元和200元,该公司要求这36个房间要在2天内粉刷完成,问人工费最低是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“※”定义一种新运算:对于任意有理数a和b,规定a※b=ab2+2ab+a.
如:1※2=1×22+2×1×2+1=9
(1)(﹣2)※3= ;
(2)若![]() ※3=16,求a的值;
※3=16,求a的值;
(3)若2※x=m,(![]() x)※3=n(其中x为有理数),试比较m,n的大小.
x)※3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六盘水市梅花山国际滑雪自建成以来,吸引大批滑雪爱好者,一滑雪者从山坡滑下,测得滑行距离y(单位:cm)与滑行时间x(单位:s)之间的关系可以近似的用二次函数来表示.
滑行时间x/s | 0 | 1 | 2 | 3 | … |
滑行距离y/cm | 0 | 4 | 12 | 24 | … |
(1)根据表中数据求出二次函数的表达式.现测量出滑雪者的出发点与终点的距离大约800m,他需要多少时间才能到达终点?
(2)将得到的二次函数图象补充完整后,向左平移2个单位,再向上平移5个单位,求平移后的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知关于x的一元二次方程x2+2x+![]() =0有两个不相等的实数根,k为正整数.
=0有两个不相等的实数根,k为正整数.
(1)求k的值;
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+![]() 的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.
的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.
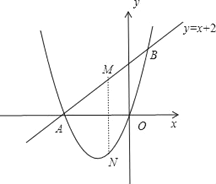
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() 与坐标轴交于
与坐标轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,且
,且![]() 点的横坐标是纵坐标的
点的横坐标是纵坐标的![]() 倍.
倍.
(1)求![]() 的值.
的值.
(2)![]() 为线段
为线段![]() 上一点,
上一点,![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 点坐标.
点坐标.
(3)如图2,![]() 为
为![]() 点右侧
点右侧![]() 轴上的一动点,以
轴上的一动点,以![]() 为直角顶点,
为直角顶点,![]() 为腰在第一象限内作等腰直角
为腰在第一象限内作等腰直角![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,当
,当![]() 点运动时,
点运动时,![]() 点的位置是否发生变化?若不变,请求出它的坐标;如果变化,请说明理由.
点的位置是否发生变化?若不变,请求出它的坐标;如果变化,请说明理由.
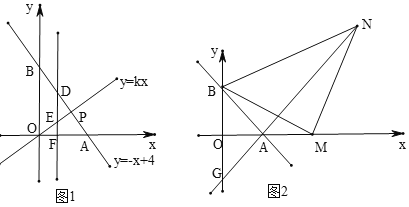
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.
(1)求证:BD=CE;
(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com