
【题目】(如图平面直角坐标系内,已知点A的坐标是(-3,0).
(1)点B的坐标为_______,点C的坐标为_____,∠BAC=______;
(2)求△ABC的面积;
(3)点P是y轴负半轴上的一个动点,连接BP交![]() 轴于点D,是否存在点P使得
轴于点D,是否存在点P使得
△ADP与△BC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.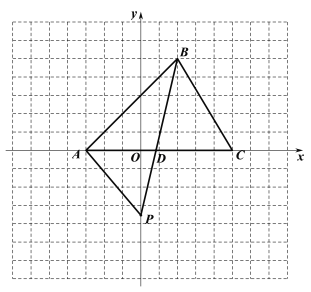
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题: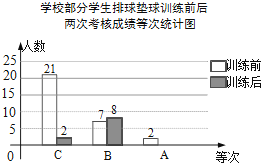
(1)抽取的学生中,训练后“A”等次的人数是多少?并补全统计图.
(2)若学校有600名学生,请估计该校训练后成绩为“A”等次的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.若a<0,则当x≤1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=![]() ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国民体质监测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况.我们队专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:


(1)在这次形体测评中,一共抽查了多少名学生?如果全市约有10万名初中生,那么全市初中生中三姿不良的学生约有多少人?
(2)请直接将两幅图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
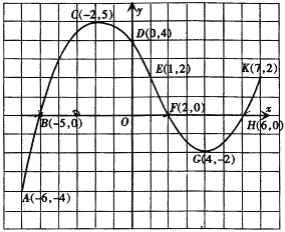
【题目】大家知道,函数图象特征与函数性质之间存在着必然联系.请根据图中的函数图象特征及表中的提示,说出此函数的变化规律.此外,你还能说出此函数的哪些性质?
序号 | 函数图象特征 | 函数变化规律 |
(1) | 曲线从点A(-6,-4)至点K(7,2) | 自变量的取值范围是______. |
(2) | 曲线与y轴交于点D(0,4) | 当x=______时,y=______. |
(3) | 曲线与x轴分别交于点B(-5,0)、F(2,0)、H(6,0) | 当x的值分别为______时,y=0. |
(4) | 曲线经过点E(1,2) | 当x=______时,y=______. |
(5) | 由左至右曲线AC呈上升状态 | 当-6≤x≤-2时,y随x的增大而______. |
(6) | 由左至右曲线CG呈下降状态 | 当______时,y随x的增大而___________. |
(7) | 由左至右曲线GK呈____________ | 当______时y随____________. |
(8) | 曲线上的最高点是C(-2,5) | 当x=______时,y有______值,且这个值为____________. |
(9) | 曲线上的最低点是____________ | 当x=______时,y有______值,且这个值为____________. |
(10) | 曲线BCF位于x轴的上方 | 当______时,y______0. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com