
甲、乙、丙三位同学进行立定跳远比赛,每人轮流跳一次称为一轮,每轮按名次从高到低分别得3分、2分、1分(没有并列名次),他们一共进行了五轮比赛,结果甲共得14分;乙第一轮得3分,第二轮得1分,且总分最低.那么丙得到的分数是( )
(A) 8分 (B) 9分 (C) 10分 (D)11分
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
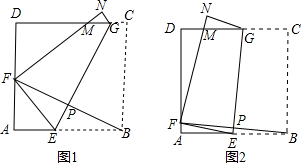 下一个正确结论(或结果):
下一个正确结论(或结果):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com