
分析 (1)设B种标号水泥的售价为x元/吨,则A种标号水泥的售价为(x+100)元/吨,根据总费用=购买A种水泥的费用+购买B种水泥的费用,即可得出关于x的一元一次方程,解之即可得出结论;
(2)根据节省的费用=原费用×a%-购买0.4a吨A种标号水泥的费用,即可得出关于a的一元二次方程,解之取其正值即可得出结论.
解答 解:(1)设B种标号水泥的售价为x元/吨,则A种标号水泥的售价为(x+100)元/吨,
根据题意得:40(x+100)+20x=28000,
解得:x=400,
x+100=500.
答:A种标号水泥的售价为500元/吨,B种标号水泥的售价为400元/吨.
(2)根据题意得:
28000×a%-0.4a×500(1-a%)=1000,
整理得:a2+40a-500=0,
解得:a1=10,a2=-50(舍去).
答:a的值为10.
点评 本题考查了一元一次方程的应用以及一元二次方程的应用,解题的关键是:(1)根据总费用=购买A种水泥的费用+购买B种水泥的费用,列出关于x的一元一次方程;(2)根据节省的费用=原费用×a%-购买0.4a吨A种标号水泥的费用,列出关于a的一元二次方程.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
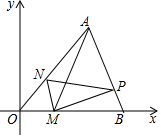 如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(6,6),O(0,0),B(8,0).点M是OB边上异于O,B的一动点,MN∥AB交OA于点N,点P是AB边上任意点,连接AM,PM,PN,BN.设点M的坐标是(t,0),△PMN的面积为S.
如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(6,6),O(0,0),B(8,0).点M是OB边上异于O,B的一动点,MN∥AB交OA于点N,点P是AB边上任意点,连接AM,PM,PN,BN.设点M的坐标是(t,0),△PMN的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在5×5的正方形网格中,每个小正方形的边长都是1个单位长度,线段AB的顶点在格点(小正方形的顶点)上.
如图,在5×5的正方形网格中,每个小正方形的边长都是1个单位长度,线段AB的顶点在格点(小正方形的顶点)上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
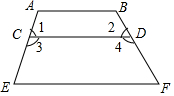 如图,给出下列论断:①∠1=∠E;②∠4=∠;③∠2+∠B=180°;④∠3+∠E=180°;⑤∠A+∠E=180°;⑥AB∥CD;⑦AB∥EF;⑧CD∥EF.请你从中选出一个论断作为题设,一个论断作为结论,组成一个真命题,至少写出三个.(格式:如果…,那么…)
如图,给出下列论断:①∠1=∠E;②∠4=∠;③∠2+∠B=180°;④∠3+∠E=180°;⑤∠A+∠E=180°;⑥AB∥CD;⑦AB∥EF;⑧CD∥EF.请你从中选出一个论断作为题设,一个论断作为结论,组成一个真命题,至少写出三个.(格式:如果…,那么…)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com