
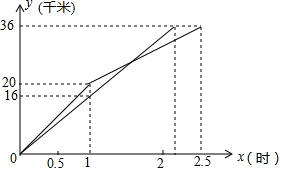
 一次国际龙舟拉力赛中,上午9时,参赛龙舟同时出发,其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点.
一次国际龙舟拉力赛中,上午9时,参赛龙舟同时出发,其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点.分析 (1)甲队在上午11时30分到达终点,共花时间2.5小时,从图象上看乙队花时间少,先到终点.从图象来看,乙队的路程与时间成正比例关系,甲队的路程与时间是一个分段函数,即在1小时内是正比例函数,在1到2.5小时是一次函数,可使用待定系数法分别求出.乙队追上甲队时,两队的路程相等,列出方程可求解;
(2)由图看出1小时之内,两队相距最远距离是4千米;乙队追上甲队后,两队的距离也可计算,相比较得出甲、乙两队在出发后1小时相距最远.
解答 解:(1)由题意知,甲上午9时出发,上午11时30分到达终点,耗时2.5小时,
根据图象可知,乙比甲先到达终点;
当0≤x≤1时,y甲=kx,
将(1,20)代入,得:20=k,即y甲=20x;
当1<x≤2.5时,y甲=kx+b,
将(1,20)、(2.5,36)代入得:
$\left\{\begin{array}{l}{k+b=20}\\{2.5k+b=36}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{32}{3}}\\{b=\frac{28}{3}}\end{array}\right.$,
∴y甲=$\left\{\begin{array}{l}{20x}&{(0≤x≤1)}\\{\frac{32}{3}x+\frac{28}{3}}&{(1<x≤2.5)}\end{array}\right.$,
设y乙=mx,
将(1,16)代入得:10=m,即y乙=16x,
令y甲=y乙,当1<x≤2.5时,$\frac{32}{3}$x+$\frac{28}{3}$=16x,得x=$\frac{7}{4}$,
故出发1小时45分钟后(或者上午10点45分)乙队追上甲队;
(2)由图象可知小时之内,两队相距最远距离是4千米,
乙队追上甲队后,两队的距离是16x-($\frac{32}{3}$x+$\frac{28}{3}$)=$\frac{16}{3}$x+$\frac{28}{3}$,
∴当x为最大,即x=$\frac{36}{16}$=$\frac{9}{4}$时,$\frac{16}{3}$x+$\frac{28}{3}$最大,
此时最大距离为$\frac{9}{4}$×$\frac{16}{3}$-$\frac{28}{3}$=$\frac{8}{3}$<4,
所以比赛过程中,甲、乙两队在出发后1小时(或者上午10时)相距最远.
点评 本题考查一次函数的应用,熟练掌握用待定系数法求一次函数关系式并将实际问题转化为一次函数的问题求解是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{10}$是无理数 | B. | $3<\sqrt{10}<4$ | ||
| C. | 10的平方根是$\sqrt{10}$ | D. | $\sqrt{10}$是10的算术平方根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
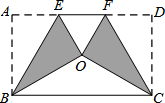 将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$.
将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com