
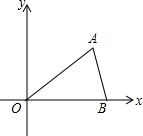
 如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A.
如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A.分析 (1)根据反比例函数y=$\frac{k}{x}$的图象过点A($\sqrt{3}$,1),可以求得k的值;
(2)过点D作DE⊥x轴于点E,根据旋转的性质求出OD=OB=2,∠BOD=60°,利用解三角形求出OE和OD的长,进而得到点D的坐标,即可作出判断点D是否在该反比例函数的图象上.
解答 解:(1)∵函数y=$\frac{k}{x}$的图象过点A($\sqrt{3}$,1),
∴k=xy=$\sqrt{3}$×1=$\sqrt{3}$;
(2)∵B(2,0),
∴OB=2,
∵△AOB绕点O逆时针旋转60°得到△COD,
∴OD=OB=2,∠BOD=60°,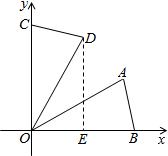 如图,过点D作DE⊥x轴于点E,则
如图,过点D作DE⊥x轴于点E,则
DE=OD•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
OE=OD•cos60°=2×$\frac{1}{2}$=1,
∴D(1,$\sqrt{3}$),
由(1)可知y=$\frac{\sqrt{3}}{x}$,
∴当x=1时,y=$\sqrt{3}$,
∴D(1,$\sqrt{3}$)在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上.
点评 本题主要考查了反比例函数图象上点的坐标特征以及图形的旋转的知识,解答本题的关键掌握旋转前后的两个图形对应边相等,对应角相等,此题难度不大.


科目:初中数学 来源: 题型:解答题
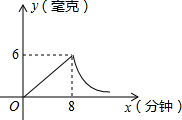 为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:
为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>0 | B. | m<0 | C. | m$>-\frac{5}{2}$ | D. | m$<-\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
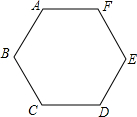 如图,已知点A、B、C、D、E、F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$.
如图,已知点A、B、C、D、E、F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 移植总数(n) | 10 | 50 | 270 | 400 | 750 | 1500 | 3500 | 7000 | 9000 |
| 成活数(m) | 8 | 47 | 235 | 369 | 662 | 1335 | 3203 | 6335 | 8118 |
| 成活的频率$\frac{m}{n}$ | 0.800 | 0.940 | 0.870 | 0.923 | 0.883 | 0.890 | 0.915 | 0.905 | 0.902 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com