
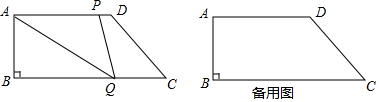
分析 (1)如图1,作高线DE,证明四边形ABED是矩形,再利用勾股定理求DC的长,在Rt△DEC中,求出
sin∠BCD=$\frac{DE}{DC}$=$\frac{4}{5}$;
(2)当四边形PDCQ为平行四边形时,点P在AD上,如图2,根据PD=CQ列方程得:6-2t=t,解出即可;
(3)分三种情况:
①当0<t≤3时,点P在边AD上,如图3,直接利用面积公式求S即可;
②当3<t≤$\frac{11}{2}$时,点P在边CD上,如图4,利用梯形面积减去三个三角形面积的差求S;
③当$\frac{11}{2}$<t≤9时,点P与C重合,Q在BC上,如图5,直接利用面积公式求S即可;
(4)画出图象,根据图象得出结论.
解答 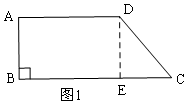 解:(1)过D作DE⊥BC于E,则∠BED=90°,
解:(1)过D作DE⊥BC于E,则∠BED=90°,
∵AD∥BC,
∴∠B+∠BAD=180°,
∵∠B=90°,
∴∠B=∠BAD=90°,
∴四边形ABED是矩形,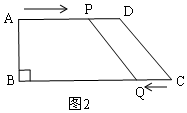
∴AD=BE=6,DE=AB=4,
∴EC=BC-BE=9-6=3,
在Rt△DEC中,由勾股定理得:DC=5,
sin∠BCD=$\frac{DE}{DC}$=$\frac{4}{5}$,
故答案为:5,$\frac{4}{5}$;
(2)由题意得:AP=2t,CQ=t,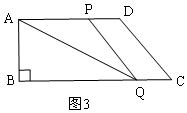
则PD=6-2t,
当四边形PDCQ为平行四边形时,如图2,
则PD=CQ,
∴6-2t=t,
∴t=2;
(3)分三种情况:
①当0<t≤3时,点P在边AD上,如图3,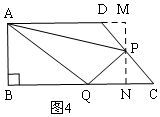
S=$\frac{1}{2}$AP•AB=$\frac{1}{2}$×4×2t=4t;
②当3<t≤$\frac{11}{2}$时,点P在边CD上,如图4,
过P作MN⊥BC,交BC于N,交AD的延长线于M,
由题意得:CQ=t,BQ=9-t,PA=2t,PD=2t-6,
∴PC=5-PD=5-(2t-6)=11-2t,
由图1得:sin∠C=$\frac{4}{5}=\frac{PN}{PC}$,
$\frac{4}{5}=\frac{PN}{11-2t}$,
PN=$\frac{4(11-2t)}{5}$,
∴PM=4-PN=4-$\frac{4(11-2t)}{5}$=$\frac{4(2t-6)}{5}$,
S=S梯形ABCD-S△PQC-S△ABQ-S△APD,
=$\frac{(6+9)×4}{2}$-$\frac{1}{2}×6×\frac{4(2t-6)}{5}$-$\frac{1}{2}$×$t×\frac{4(11-2t)}{5}$-$\frac{1}{2}×(9-t)×4$=$\frac{4}{5}{t}^{2}-\frac{36}{5}t+\frac{132}{5}$;
③当$\frac{11}{2}$<t≤9时,点P与C重合,Q在BC上,如图5,
S=$\frac{1}{2}×t×4$=2t;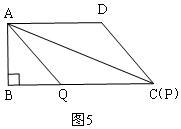
综上所述,S与t的函数关系式为:S=$\left\{\begin{array}{l}{4t(0<t≤3)}\\{\frac{4}{5}{t}^{2}-\frac{36}{5}t+\frac{132}{5}(3<t≤\frac{11}{2})}\\{2t(\frac{11}{2}<t≤9)}\end{array}\right.$.
(4)如图6,S=$\frac{4}{5}{t}^{2}-\frac{36}{5}t+\frac{132}{5}$;
S的最小值为:$\frac{4×\frac{4}{5}×\frac{132}{5}-(-\frac{36}{5})^{2}}{4×\frac{4}{5}}$=$\frac{51}{5}$,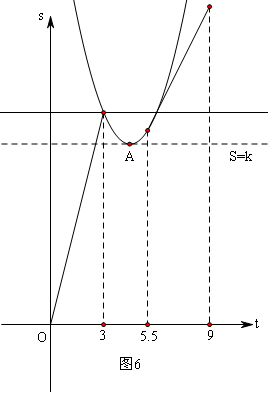
当t=3时,S=4×3=12,
∴则k的取值范围是:$\frac{51}{5}$<k<12.
故答案为:$\frac{51}{5}$<k<12.
点评 本题是四边形的综合题,考查了梯形的性质、平行四边形的性质、三角函数、面积的求法和函数问题,将四边形与二次函数、一次函数相结合,综合性较强,利用动点运动到不同位置,根据数形结合解决问题,本题还要注意点P运动结束后,点Q还继续运动,即当$\frac{11}{2}$<t≤9时,点P与C重合,Q在BC上.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
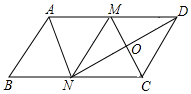 如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.
如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
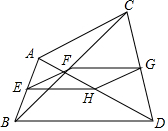 如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.
如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
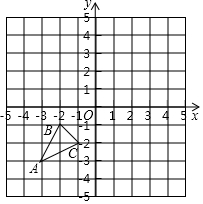 如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是平面直角坐标系上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是平面直角坐标系上三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
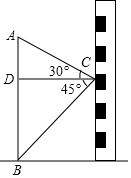 如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果精确到0.1米)
如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com