
分析 设a+b+c=d,则有a=d-(b+c),b=d-(a+c),c=d-(a+b),然后把它们代入到所求分式,化简后就可解决问题.
解答 解:设a+b+c=d,则有a=d-(b+c),b=d-(a+c),c=d-(a+b).
∵$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$=1,
∴$\frac{{a}^{2}}{b+c}$+$\frac{{b}^{2}}{c+a}$+$\frac{{c}^{2}}{a+b}$=$\frac{a}{b+c}$•a+$\frac{b}{c+a}$•b+$\frac{c}{a+b}$•c
=$\frac{a}{b+c}$•[d-(b+c)]+$\frac{b}{c+a}$•[d-(a+c)]+$\frac{c}{a+b}$•[d-(a+b)]
=$\frac{a}{b+c}$•d-a+$\frac{b}{c+a}$•d-b+$\frac{c}{a+b}$•d-c
=d($\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$)-(a+b+c)
=d($\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$)-d
=d($\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$-1)
=0,
故答案为:0.
点评 本题考查了求分式的值,有一定的技巧性,而解决本题的关键是把a+b+c看成一个整体,从而把所求分式与条件联系起来.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
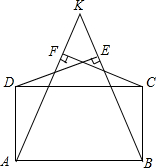 如图,K为矩形ABCD的CD边外的一点,连线KA、KB均与CD边相交,过D作KB的垂线,垂足为E,过C作KA的垂线,垂足为F,若DE、CF交于点M,求证:KM⊥AB.
如图,K为矩形ABCD的CD边外的一点,连线KA、KB均与CD边相交,过D作KB的垂线,垂足为E,过C作KA的垂线,垂足为F,若DE、CF交于点M,求证:KM⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
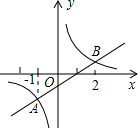 如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )
如图,一次函数与反比例函数的图象相交于A、B两点,则使得反比例函数值小于一次函数值的x的取值范围是( )| A. | x<-1 | B. | -1<x<0或x>2 | C. | x<-1或0<x<2 | D. | x>2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com