
�Ķ����ϣ�
����˵������ʽ x2+1 + (x-3)2+4 �ļ������壬����������Сֵ��
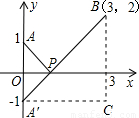
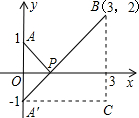
�⣺ x2+1 + (x-3)2+4 = (x-0)2+12 + (x-3)2+22 ����ͼ������ƽ��ֱ������ϵ����P��x��0����x����һ�㣬�� (x-0)2+12 ���Կ��ɵ�P���A��0��1���ľ��룬 (x-3)2+22 ���Կ��ɵ�P���B��3��2���ľ��룬����ԭ����ʽ��ֵ���Կ����߶�PA��PB����֮�ͣ�������Сֵ����PA+PB����Сֵ��
���A����x��ĶԳƵ�ΪA�䣬��PA=PA�䣬��ˣ���PA+PB����Сֵ��ֻ����PA��+PB����Сֵ������A�䡢B���ֱ�߶ξ�����̣�����PA��+PB����СֵΪ�߶�A��B�ij��ȣ�Ϊ�ˣ�����ֱ��������A��CB����ΪA��C=3��CB=3������A��B=3 2 ����ԭʽ����СֵΪ3 2 ��
���������Ķ����ϣ�����������⣺
��1������ʽ (x-1)2+1 + (x-2)2+9 ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��1��1������B ��2��3���ľ���֮�ͣ�����д��B�����꣩
��2������ʽ x2+49 + x2-12x+37 ����СֵΪ��
��1����2��3����2��10
���������⣺��1����ԭʽ��Ϊ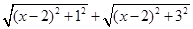 ����ʽ��
����ʽ��
�����ʽ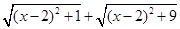 ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��1��1������B��2��3���ľ���֮�ͣ�
��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��1��1������B��2��3���ľ���֮�ͣ�
�ʴ�Ϊ��2��3����
��2����ԭʽ��Ϊ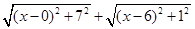 ����ʽ��
����ʽ��
���������ʽ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��0��7������B��6��1���ľ���֮�ͣ�
��ͼ��ʾ�����A����x��ĶԳƵ�ΪA�䣬��PA=PA�䣬
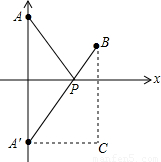
��PA+PB����Сֵ��ֻ����PA��+PB����Сֵ������A�䡢B���ֱ�߶ξ�����̣�
��PA��+PB����СֵΪ�߶�A��B�ij��ȣ�
��A��0��7����B��6��1��
��A�䣨0��-7����A��C=6��BC=8��
��A��B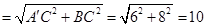 ��
��
1���Ȱ�ԭʽ��Ϊ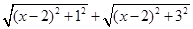 ����ʽ���ٸ����������������Ӽ��ɵó����ۣ�
����ʽ���ٸ����������������Ӽ��ɵó����ۣ�
��2���Ȱ�ԭʽ��Ϊ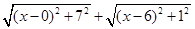 ����ʽ���ʵó��������ʽ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��0��7������B��6��1���ľ���֮�ͣ��ٸ���������ϵ��������㣬���ù��ɶ����ó����ۼ��ɣ�
����ʽ���ʵó��������ʽ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��0��7������B��6��1���ľ���֮�ͣ��ٸ���������ϵ��������㣬���ù��ɶ����ó����ۼ��ɣ�


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
 ��2012•ʮ�ߣ��Ķ����ϣ�
��2012•ʮ�ߣ��Ķ����ϣ�| x2+1 |
| (x-3)2+4 |
| x2+1 |
| (x-3)2+4 |
| (x-0)2+12 |
| (x-3)2+22 |
| (x-0)2+12 |
| (x-3)2+22 |
| 2 |
| 2 |
| (x-1)2+1 |
| (x-2)2+9 |
| x2+49 |
| x2-12x+37 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012����б�ҵ��ѧ���ԣ�����ʮ�߾�����ѧ���������� ���ͣ������
�Ķ����ϣ�
����˵������ʽ x2+1 + (x-3)2+4 �ļ������壬����������Сֵ��
�⣺ x2+1 + (x-3)2+4 =" (x-0)2+12" + (x-3)2+22 ����ͼ������ƽ��ֱ������ϵ����P��x��0����x����һ�㣬�� (x-0)2+12 ���Կ��ɵ�P���A��0��1���ľ��룬 (x-3)2+22 ���Կ��ɵ�P���B��3��2���ľ��룬����ԭ����ʽ��ֵ���Կ����߶�PA��PB����֮�ͣ�������Сֵ����PA+PB����Сֵ��
���A����x��ĶԳƵ�ΪA�䣬��PA=PA�䣬��ˣ���PA+PB����Сֵ��ֻ����PA��+PB����Сֵ������A�䡢B���ֱ�߶ξ�����̣�����PA��+PB����СֵΪ�߶�A��B�ij��ȣ�Ϊ�ˣ�����ֱ��������A��CB����ΪA��C=3��CB=3������A��B="3" 2 ����ԭʽ����СֵΪ3 2 ��
���������Ķ����ϣ�����������⣺
��1������ʽ (x-1)2+1 + (x-2)2+9 ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��1��1������B ��2��3���ľ���֮�ͣ�����д��B�����꣩
��2������ʽ x2+49 + x2-12x+37 ����СֵΪ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�п����� ���ͣ������
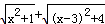 �ļ������壬����������Сֵ��
�ļ������壬����������Сֵ�� ����ͼ������ƽ��ֱ������ϵ����P ��x ��0 ����x ����һ�㣬��
����ͼ������ƽ��ֱ������ϵ����P ��x ��0 ����x ����һ�㣬�� 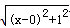 ���Կ��ɵ�P ���A ��0 ��1 ���ľ��룬
���Կ��ɵ�P ���A ��0 ��1 ���ľ��룬 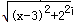 ���Կ��ɵ�P ���B ��3 ��2 ���ľ��룬����ԭ����ʽ��ֵ���Կ����߶�PA ��PB ����֮�ͣ�������Сֵ����PA+PB ����Сֵ��
���Կ��ɵ�P ���B ��3 ��2 ���ľ��룬����ԭ����ʽ��ֵ���Կ����߶�PA ��PB ����֮�ͣ�������Сֵ����PA+PB ����Сֵ��
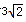
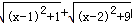 ��ֵ���Կ���ƽ��ֱ������ϵ�е�P ��x ��0 �����A(1 ��1)����B ( )�ľ���֮�ͣ�����д��B �����꣩
��ֵ���Կ���ƽ��ֱ������ϵ�е�P ��x ��0 �����A(1 ��1)����B ( )�ľ���֮�ͣ�����д��B �����꣩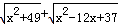 ����СֵΪ( )��
����СֵΪ( )��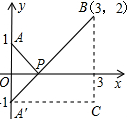
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�����ʡʮ�����п���ѧ�Ծ��������棩 ���ͣ������
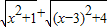 �ļ������壬����������Сֵ��
�ļ������壬����������Сֵ��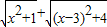 =
=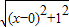 +
+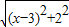 ����ͼ������ƽ��ֱ������ϵ����P��x��0����x����һ�㣬��
����ͼ������ƽ��ֱ������ϵ����P��x��0����x����һ�㣬��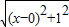 ���Կ��ɵ�P���A��0��1���ľ��룬
���Կ��ɵ�P���A��0��1���ľ��룬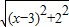 ���Կ��ɵ�P���B��3��2���ľ��룬����ԭ����ʽ��ֵ���Կ����߶�PA��PB����֮�ͣ�������Сֵ����PA+PB����Сֵ��
���Կ��ɵ�P���B��3��2���ľ��룬����ԭ����ʽ��ֵ���Կ����߶�PA��PB����֮�ͣ�������Сֵ����PA+PB����Сֵ��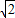 ����ԭʽ����СֵΪ3
����ԭʽ����СֵΪ3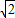 ��
��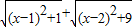 ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��1��1������B______�ľ���֮�ͣ�����д��B�����꣩
��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��1��1������B______�ľ���֮�ͣ�����д��B�����꣩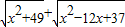 ����СֵΪ______��
����СֵΪ______��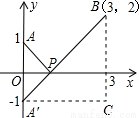
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com