
【题目】如图,已知在△ABC中,DE∥CA,∠1=∠2,∠3=∠4,∠BAC=84°.求∠EDA的度数.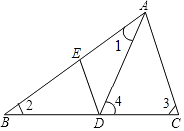
【答案】解:∵∠4是△ABD的一个外角,
∴∠4=∠1+∠2,
设∠1=∠2=x,则∠4=∠3=2x,
在△ADC中,∠4+∠3+∠DAC=180°,
∴∠DAC=180﹣4x,
∵∠BAC=∠1+∠DAC,
∴84=x+180﹣4x,
x=32,
∴∠DAC=180﹣4x=180﹣4×32=52°,
∵DE∥CA,
∴∠EDA=∠DAC=52°
【解析】设∠1=∠2=x,根据外角定理得∠4=∠3=2x,由三角形的内角和定理表示∠DAC=180-4x,利用∠BAC=84°列等式可得结论.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对三角形的内角和外角的理解,了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
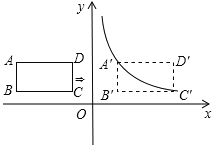
【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(![]() ,
,![]() ),AB=1,AD=2.
),AB=1,AD=2.
(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数![]() (
(![]() )的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
)的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明. 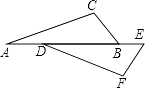
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( ) 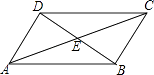
A.6
B.12
C.20
D.24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com