
分析 (1)将m=1代入原方程,再根据根的判别式即可得出△>0,由此即可得出:当m=1时,方程有两个不相等的实数根;
(2)找出倒数等于本身的数,再将其代入原方程中即可得出关于m的一元一次方程,解之即可得出m的值.
解答 解:(1)当m=1时,原方程为x2+2x+$\frac{1}{2}$=0,
∵△=22-4×1×$\frac{1}{2}$=2>0,
∴当m=1时,方程有两个不相等的实数根;
(2)倒数是它本身的数是±1.
当x=1时,有1+(m+1)+$\frac{1}{2}$=0,
解得:m=-$\frac{5}{2}$;
当x=-1时,有1-(m+1)+$\frac{1}{2}$=0,
解得:m=$\frac{1}{2}$.
∴若方程一个实数根的倒数恰是它本身,则m的值为-$\frac{5}{2}$或$\frac{1}{2}$.
点评 本题考查了根的判别式、一元二次方程的解以及倒数,熟练掌握“当根的判别式△>0时,方程有两个不相等的实数根”是解题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:解答题
| 模球次数 | 15 | 80 | 180 | 600 | 1000 |
| 模到白球次数 | 5 | 21 | 39 | 250 | |
| 模到白球的频率 | 0.33 | 0.26 | 0.21 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
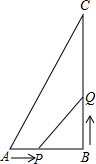 在三角形ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.
在三角形ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
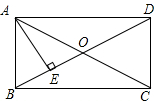 如图,矩形ABCD中,O是两对角线的交点,AE⊥BD,垂足为E.若OD=2OE,AE=$\sqrt{3}$,则AD的长为2$\sqrt{3}$.
如图,矩形ABCD中,O是两对角线的交点,AE⊥BD,垂足为E.若OD=2OE,AE=$\sqrt{3}$,则AD的长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.
如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com