考点:二次函数的三种形式
专题:
分析:(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;
(2)根据二次函数的性质,利用二次函数的顶点式即可求出抛物线的顶点坐标与对称轴;
(3)把y=0代入y=2x2-8x+6,解方程求出x的值,从而得到抛物线与x轴的交点坐标;把x=0代入y=2x2-8x+6,求出y的值,从而得到抛物线与y轴的交点坐标.
解答:解:(1)y=2x2-8x+6=2(x2-4x+4)-8+6=2(x-2)2-2;
(2)∵y=2(x-2)2-2,
∴抛物线的顶点坐标是:(2,-2);对称轴是:x=2;
(3)∵y=2x2-8x+6,
∴当y=0时,2x2-8x+6=0,解得x1=1,x2=3,
∴抛物线与x轴的交点坐标为(1,0),(3,0);
当x=0时,y=6,
∴抛物线与y轴的交点坐标为(0,6).
故答案为y=2(x-2)2-2;(2,-2),x=2.
点评:本题考查了二次函数的解析式有三种形式:
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
(2)顶点式:y=a(x-h)2+k;
(3)交点式(与x轴):y=a(x-x1)(x-x2).
同时考查了二次函数的性质以及抛物线与坐标轴交点坐标的求法.



 阅读快车系列答案
阅读快车系列答案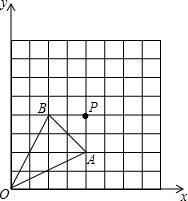 △OAB在坐标系中的位置如图所示.
△OAB在坐标系中的位置如图所示.