
【题目】甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x kg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元, y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
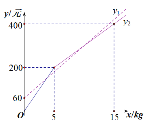
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5 kg后,超过的部分价格优惠是打五折
D.若顾客采摘12 kg草莓,那么到甲园或乙园的总费用相同
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
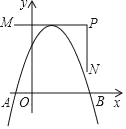
【题目】如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则a﹣b+c的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初一、初二年级各有500名学生,为了解两个年级的学生对消防安全知识的掌握情况,学校从初一、初二年级各随机抽取20名学生进行消防安全知识测试,满分100分,成绩整理分析过程如下,请补充完整:
(收集数据)
初一年级20名学生测试成绩统计如下:
78 56 74 81 95 75 87 70 75 90 75 79 86 60 54 80 66 69 83 97
初二年级20名学生测试成绩不低于80,但是低于90分的成绩如下:
83 86 81 87 80 81 82
(整理数据)按照如下分数段整理、描述两组样本数据:
成绩 |
|
|
|
|
|
初一 | 2 | 3 | 7 | 5 | 3 |
初二 | 0 | 4 | 5 | 7 | 4 |
(分析数据)两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
初一 | 76.5 | 76.5 |
| 132.5 |
初二 | 79.2 |
| 74 | 100.4 |
(1)直接写出![]() ,
,![]() 的值;
的值;
(2)根据抽样调查数据,估计初一年级消防安全知识测试成绩在70分及其以上的大约有多少人?
(3)通过以上分析,你认为哪个年级对消防安全知识掌握得更好,并说明推断的合理性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交与A(4,-2),B(-2,n)两点,与
的图像交与A(4,-2),B(-2,n)两点,与![]() 轴交与点C.
轴交与点C.
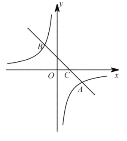
(1)求![]() ,n的值;
,n的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)点A关于![]() 轴对称得到点A’,连接A’B,A’C,求△A’BC的面积.
轴对称得到点A’,连接A’B,A’C,求△A’BC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》里有一道著名算题:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二乘、问上、下禾实一乘各几何?”大意是:3捆上等谷子结出的粮食,再加.上六斗,相当于10捆下等谷子结出的粮食.5捆下等谷子结出的粮食,再加上一斗,相当于2捆上等谷子结出的粮食.问:上等谷子和下等谷子每捆能结出多少斗粮食?请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
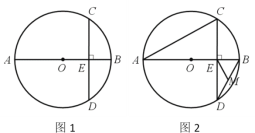
【题目】已知AB是⊙O的直径,C是⊙O上的一点(不与点A,B重合),过点C作AB的垂线交⊙O于点D,垂足为E点.
(1)如图1,当AE=4,BE=2时,求CD的长度;
(2)如图2,连接AC,BD,点M为BD的中点.求证:ME⊥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边
的边![]() 在正方形
在正方形![]() 的边
的边![]() 上,连结
上,连结![]() 、
、![]() .
.
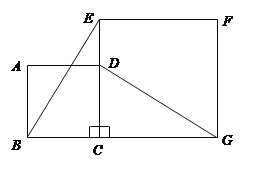
(1)观察猜想![]() 与
与![]() 之间的大小关系,并证明你的结论;
之间的大小关系,并证明你的结论;
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,说出旋转过程;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
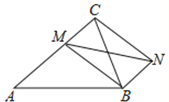
【题目】如图,已知在△ABC中,AB=AC=13,BC=10,点M是AC边上任意一点,连接MB,以MB、MC为邻边作平行四边形MCNB,连接MN,则MN的最小值是______
查看答案和解析>>
科目:初中数学 来源: 题型:
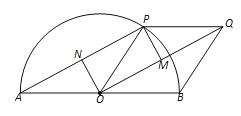
【题目】如图,已知AB为半圆O的直径,P为半圆上的一个动点(不含端点),以OP、OB为一组邻边作POBQ,连接OQ、AP,设OQ、AP的中点分别为M、N,连接PM、ON.
(1)试判断四边形OMPN的形状,并说明理由.
(2)若点P从点B出发,以每秒15°的速度,绕点O在半圆上逆时针方向运动,设运动时间为ts.
①试求:当t为何值时,四边形OMPN的面积取得最大值?并判断此时直线PQ与半圆O的位置关系(需说明理由);
②是否存在这样的t,使得点Q落在半圆O内?若存在,请直接写出t的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com