练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．求下列各式中的x．
    （1）x2=81；   　　　　　　　　　　  
    （2）16x2-25=0．

    分析 （1）两边开方，即可得出两个一元一次方程，求出方程的解即可；
    （2）先分解因式，即可得出两个一元一次方程，求出方程的解即可．

    解答 解：（1）两边开方得：x=±9，
    即x1=9，x2=-9；

    （2）分解因式得：（4x+5）（4x-5）=0，
    4x+5=0，4x-5=0，
    x1=-$\frac{5}{4}$，x2=$\frac{5}{4}$．

    点评 本题考查了解一元二次方程的应用，能把一元二次方程转化成一元一次方程是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．已知△ABC中，AC=6cm，BC=8cm，AB=10cm，CD为AB边上的高．动点P从点A出发，沿着△ABC的三条边逆时针走一圈回到A点，速度为2cm/s，设运动时间为ts．
    （1）求CD的长；
    （2）t为何值时，△ACP为等腰三角形？
    （3）若M为BC上一动点，N为AB上一动点，是否存在M，N使得AM+MN的值最小，如果有请尺规作出图形（不必求最小值），如果没有请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列说法错误的是（　　）
    A．2x2-3xy-1是二次三项式B．-x+1是多项式
    C．-$\frac{2}{3}$πxy2的系数是-$\frac{2}{3}$πD．x与π是同类项

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

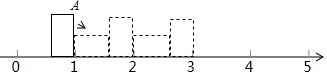
    9．如图，在数轴上放置一个长方形块，长方形的长为$\frac{3}{4}$，宽为$\frac{1}{3}$．此时将长方形沿数轴正方向做顺时针的翻动．长方形所在的初始位置如图中实线所示，沿A点（如图所示）做数轴的垂线，在数轴上所对应的数字是1．

    翻动次数A点在数轴上对应的数字
    　1　1+$\frac{3}{4}$
    　2　1+$\frac{3}{4}$+0
    　3
    　4
    （1）第3次翻动长方形块后，A点在数轴上所对应的数字表示是$\frac{25}{12}$
    （2）第8次翻动长方形块后，A点在数轴上所对应的数字表示是5$\frac{1}{3}$
    （3）第101次翻动长方形块后，A点在数轴上所对应的数字表示是55$\frac{11}{12}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．若|x-3|+（y+6）2+$\sqrt{z+2}$=0，求代数式$\frac{x}{y-z}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知方程6x-9=10x-45与方程3a-1=3（x+a）-2a的解相同，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

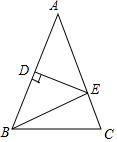    13．如图，△ABC中，AB=AC，DE垂直平分AB，D为垂足交AC于E．
    （1）若∠A=50°，求∠EBC的度数．
    （2）若AB=8，△BEC的周长是11，求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，点A（-10，0），B（-6，0），点C在y轴的正半轴上，∠CBO=45°，CD∥AB，∠CDA=90°．点P从点Q（8，0）出发，沿x轴向左以每秒1个单位长的速度向点A匀速运动，运动时间为t秒．
    （1）求点C的坐标．
    （2）当∠BCP=15°时，求t的值．
    （3）以PC为直径作圆，当该圆与四边形ABCD的边（或边所在的直线）相切时，求t的值．

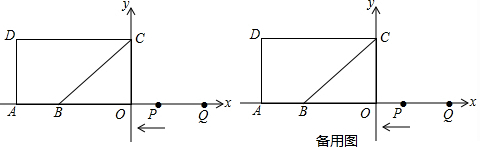
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．想一想：确定正比例函数表达式需要几个条件？2个；确定一次函数表达式需耍几个条件？1个．

    查看答案和解析>>

    同步练习册答案