
 如图,在平面直角坐标系中,已知点M(2,-3)、N(6,-3),连接MN,如果点P在直线y=-x+1上,且点P到直线MN的距离不小于1,那么称点P是线段MN的“疏远点”.
如图,在平面直角坐标系中,已知点M(2,-3)、N(6,-3),连接MN,如果点P在直线y=-x+1上,且点P到直线MN的距离不小于1,那么称点P是线段MN的“疏远点”.分析 (1)求出A到MN的距离,再判断即可;
(2)根据“疏远点”的意义求出b的范围,再代入求出a的范围即可;
(3)根据“疏远点”的意义得出S△MNP=$\frac{1}{2}$×4×|-a-(-3)|,再去掉绝对值符号即可.
解答 解:(1)点A(2,-1)是线段MN的“疏远点”,并说明理由
理由是:∵M(2,-3)、N(6,-3),A(2,-1),
∴A到直线MN的距离为-1-(-3)=2>1,
∵点P到直线MN的距离不小于1,那么称点P是线段MN的“疏远点”,
∴点A(2,-1)是线段MN的“疏远点”;
(2)∵点P(a,b)是线段MN的“疏远点”,M(2,-3)、N(6,-3),
∴|b-(-3)|≥1,
∴b≥-1或b≤-4,
代入y=-x+1得:-a+1≥-1或-a+1≤-4,
解得:a≤2或a≥3,
即a的取值范围是a≤2或a≥3;
(3)∵M(2,-3)、N(6,-3),
∴MN=6-2=4,
∴S△MNP=$\frac{1}{2}$×4×|-a-(-3)|
=$\left\{\begin{array}{l}{8-2a(a≤2)}\\{2a-8(a≥3)}\end{array}\right.$
S△MNP的最小值是$\frac{1}{2}×4×1$=2.
点评 本题考查了一次函数图象上点的特征,一次函数的性质等知识点,能根据“疏远点”的意义列出算式是解此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
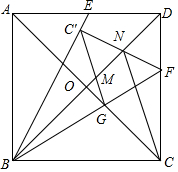 在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是6-$\frac{6}{5}\sqrt{5}$.
在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是6-$\frac{6}{5}\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠B=2∠C | B. | ∠A+∠B=∠C | C. | ∠A:∠B:∠C=1:4:5 | D. | ∠A=37°,∠B=53° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
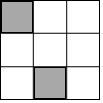 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )
如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )| A. | $\frac{5}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 45000名学生是总体 | |
| B. | 1500名学生的身高是总体的一个样本 | |
| C. | 每名学生是总体的一个个体 | |
| D. | 以上调查是全面调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,AB=4$\sqrt{2}$,AC与BD相交于点O,点P是AC上一动点,点E为射线BC上的一点,且PB=PE,过点E作EF⊥AC,垂足为点F.
如图,在正方形ABCD中,AB=4$\sqrt{2}$,AC与BD相交于点O,点P是AC上一动点,点E为射线BC上的一点,且PB=PE,过点E作EF⊥AC,垂足为点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com