
【题目】已知关于 x 的一元二次方程 x![]() 2k 1 x k
2k 1 x k![]() k 1 0 有实数根.
k 1 0 有实数根.
(1)求k 的取值范围;
(2)若此方程的两实数根![]() ,
,![]() 满足
满足![]()
![]() 11 ,求k 的值.
11 ,求k 的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据方程有实数根得出△=[-(2k-1)]2-4×1×(k2+k-1)=-8k+5≥0,解之可得.
(2)利用根与系数的关系可用k表示出x1+x2和x1x2的值,根据条件可得到关于k的方程,可求得k的值,注意利用根的判别式进行取舍.
解:(1)∵关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根,
∴△≥0,即[-(2k-1)]2-4×1×(k2+k-1)=-8k+5≥0,
解得k≤![]() .
.
(2)由根与系数的关系可得x1+x2=2k-1,x1x2=k2+k-1,
∴x12+x22=(x1+x2)2-2x1x2=(2k-1)2-2(k2+k-1)=2k2-6k+3,
∵x12+x22=11,
∴2k2-6k+3=11,解得k=4,或k=-1,
∵k≤![]() ,
,
∴k=4(舍去),
∴k=-1.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
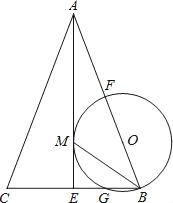
【题目】如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)判断AE与⊙O的位置关系,并说明理由;
(2)若BC=6,AC=4CE时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,求△PCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图,已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.那么在这次评比中,被评为优秀(分数大于或等于80分为优秀,且分数为整数)的调查报告有( )

A.18篇B.24篇C.25篇D.27篇
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的边长为2cm,∠A=60°,点M从点A出发,以1cm/s的速度向点B运动,点N从点A同时出发,以2cm/s的速度经过点D向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动.则△AMN的面积y(cm2)与点M运动的时间t(s)的函数的图象大致是( )

A. 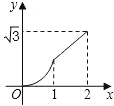 B.
B. 
C.  D.
D. 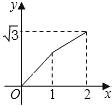
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4![]() ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
(1)求抛物线C的函数表达式;
(2)若抛物线C/与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
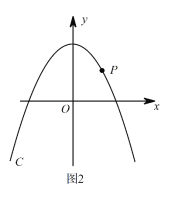
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C/上的对应点P/,设M是C上的动点,N是C/上的动点,试探究四边形PMP/N能否成为正方形?若能,请直接写出m的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 点
点![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 与点
与点![]() 不重合),过动点
不重合),过动点![]() 作
作![]() 交
交![]() 于点
于点![]()

(1)若![]() 与
与![]() 相似,则
相似,则![]() 是多少度?
是多少度?
(2)试问:当![]() 等于多少时,
等于多少时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
(3)若以线段![]() 为直径的圆和以线段
为直径的圆和以线段![]() 为直径的圆相外切,求线段
为直径的圆相外切,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中,设单元正方形边长为1.
(1)已知△ABC的顶点都在格点上,请直接写出△ABC的面积S= ;
(2)请以点O为位似中心,相似比为2,在方格纸中将△ABC放大,画出放大后的图形△A′B'C';
(3)求△A′B'C′的面积S′.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com