
点A的坐标为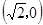 ,把点A绕着坐标原点顺时针旋转135°到点B,那么点B的坐标是 .
,把点A绕着坐标原点顺时针旋转135°到点B,那么点B的坐标是 .
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
平面直角坐标系xOy中,抛物线![]() 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
(1) 求此抛物线的解析式;
(2) 若此抛物线的对称轴上的点P满足∠APB=∠ACB,求点P的坐标;
(3) Q为线段BD上一点,点A关于∠AQB的平分线的对称点为![]() ,若
,若![]() ,求点Q的坐标和此时△
,求点Q的坐标和此时△![]() 的面积.
的面积.
【解析】此题考核二次函数的的解析式的求解,以及运用图像与坐标轴的交点问题,能求解得到a,c关系式,然后把原解析式化简为关于a的表达式,![]() 然后借助于根的情况得到点B的坐标,从而得到与坐标轴y轴点C的坐标,得到a的值,得到求解。最后一问利用点A关于∠AQB的平分线的对称点为,对称性求解得到点的坐标,进而求解面积。
然后借助于根的情况得到点B的坐标,从而得到与坐标轴y轴点C的坐标,得到a的值,得到求解。最后一问利用点A关于∠AQB的平分线的对称点为,对称性求解得到点的坐标,进而求解面积。
查看答案和解析>>
科目:初中数学 来源:2013届福建仙游高峰初级中学九年级上学期期中考试数学试题(带解析) 题型:填空题
点A的坐标为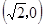 ,把点A绕着坐标原点顺时针旋转135°到点B,那么点B的坐标是 .
,把点A绕着坐标原点顺时针旋转135°到点B,那么点B的坐标是 .
查看答案和解析>>
科目:初中数学 来源:2009年江苏省中考统考数学模拟试卷(2)(解析版) 题型:解答题
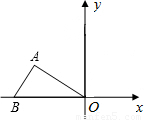
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省泰州市海陵区九年级二模数学卷(解析版) 题型:解答题
平面直角坐标系xOy中,抛物线 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,
0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,
0),OB=OC,抛物线的顶点为D.
(1) 求此抛物线的解析式;
(2) 若此抛物线的对称轴上的点P满足∠APB=∠ACB,求点P的坐标;
(3) Q为线段BD上一点,点A关于∠AQB的平分线的对称点为 ,若
,若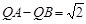 ,求点Q的坐标和此时△
,求点Q的坐标和此时△ 的面积.
的面积.
【解析】此题考核二次函数的的解析式的求解,以及运用图像与坐标轴的交点问题,能求解得到a,c关系式,然后把原解析式化简为关于a的表达式,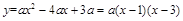 然后借助于根的情况得到点B的坐标,从而得到与坐标轴y轴点C的坐标,得到a的值,得到求解。最后一问利用点A关于∠AQB的平分线的对称点为,对称性求解得到点的坐标,进而求解面积。
然后借助于根的情况得到点B的坐标,从而得到与坐标轴y轴点C的坐标,得到a的值,得到求解。最后一问利用点A关于∠AQB的平分线的对称点为,对称性求解得到点的坐标,进而求解面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com