
分析 (1)根据一元二次方程根与系数的关系及完全平方公式,即可求出sinA的值;
(2)根据根的判别式首先求出k的值,然后分两种情况:①∠A是底角;②∠A是顶角,分别求出△ABC的第三边的长度.
解答 解:(1)设关于x的方程9x2-9sinA•x-2=0的两根为x1,x2,
则x1+x2=sinA,x1•x2=-$\frac{2}{9}$.
∴x12+x22=(x1+x2)2-2x1•x2=sin2A+$\frac{4}{9}$.
∵方程9x2-9sinA•x-2=0的两根的平方和是1,
∴sin2A+$\frac{4}{9}$=1,
∴sinA=±$\frac{\sqrt{5}}{3}$,
∵∠A为锐角,
∴sinA=$\frac{\sqrt{5}}{3}$;
(2)依题意,知m、n是方程y2-6y+k2+4k+13=0的两根,
则△≥0,
∴36-4(k2+4k+13)≥0,
∴-(k+2)2≥0,
∴(k+2)2≤0,
又∵(k+2)2≥0,
∴k=-2.
把k=-2代入方程,得y2-6y+9=0,
解得y=3,
∴m=n=3,
∴△ABC是等腰三角形.
分两种情况:①∠A是底角;②∠A是顶角.
①当∠A是底角时,如图,△ABC中,AB=BC=3,作底边AB上的高BD,则AB=2AD.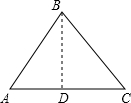 在直角△ABD中,
在直角△ABD中,
∵sinA=$\frac{\sqrt{5}}{3}$,
∴$\frac{BD}{AB}$=$\frac{\sqrt{5}}{3}$,
∴BD=$\sqrt{5}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=2,
∴AC=4;
②当∠A是顶角时,如图,△ABC中,AB=AC=3,作腰AC上的高BD. 在直角△ABD中,∵sinA=$\frac{\sqrt{5}}{3}$,
在直角△ABD中,∵sinA=$\frac{\sqrt{5}}{3}$,
∴$\frac{BD}{AB}$=$\frac{\sqrt{5}}{3}$,
∴BD=$\sqrt{5}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=2,
∴CD=AC-AD=1.
在直角△ABD中,∵∠BDC=90°,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{6}$.
综上可知,△ABC的第三边的长度为4或$\sqrt{6}$.
点评 本题主要考查了根的判别式,根与系数的关系,等腰三角形的性质,三角函数的定义,综合性强,难度较大.


科目:初中数学 来源: 题型:选择题
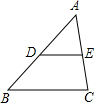 如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=3DE;②△ADE∽△ABC;$③\frac{AD}{AE}=\frac{AB}{AC}$;④$\frac{三角形ADE面积}{四边形BCED的面积}=\frac{1}{3}$,其中正确的有( )
如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=3DE;②△ADE∽△ABC;$③\frac{AD}{AE}=\frac{AB}{AC}$;④$\frac{三角形ADE面积}{四边形BCED的面积}=\frac{1}{3}$,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 把一个斜边长为10cm的含45°角的直角三角板放在三条互相平行的直线a,b,c,且直线a,b的距离和直线b,c之间的距离都是d,求d的值.
把一个斜边长为10cm的含45°角的直角三角板放在三条互相平行的直线a,b,c,且直线a,b的距离和直线b,c之间的距离都是d,求d的值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
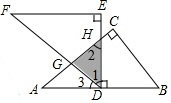 如图所示,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE⊥AB交AC于点H,DF交AC于点G,则重叠部分(△DGH)的面积为$\frac{75}{16}$.
如图所示,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE⊥AB交AC于点H,DF交AC于点G,则重叠部分(△DGH)的面积为$\frac{75}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 所有有理数都有算术平方根 | B. | 一个数的算术平方根总是正数 | ||
| C. | 当a<0时,$\sqrt{a}$没有意义 | D. | $\sqrt{a}$可以是正数,也可以是负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
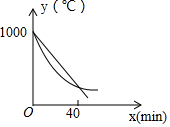 某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过xmin时,A、B两组材料的温度分别为yA℃、yB℃;yA、yB与x的函数关系式分别为yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分图象如图所示,当x=40时,两组材料的温度相同).
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过xmin时,A、B两组材料的温度分别为yA℃、yB℃;yA、yB与x的函数关系式分别为yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分图象如图所示,当x=40时,两组材料的温度相同).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
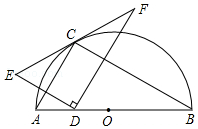 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:( )
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:( )| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com