
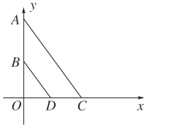
【题目】如图8,在平面直角坐标系xOy中,A(0,8),B(0,4),点C在x轴的正半轴上,点D为OC的中点.
(1)当BD与AC的距离等于2时,求线段OC的长;
(2)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线BD的解析式.
【答案】(1)![]() ;(2) y=-x+4.
;(2) y=-x+4.
【解析】
(1)作BF⊥AC于点F,取AB的中点G,确定出G坐标,由平行线间的距离相等求出BF的长,在直角三角形ABF中,利用斜边上的中线等于斜边的一半求出FG的长,进而确定出三角形BFG为等边三角形,即∠BAC=30°,设OC=x,则有AC=2x,利用勾股定理表示出OA,根据OA的长求出x的值,即可确定出C坐标;
(2)根据平行四边形的性质可得出DE⊥OC,利用等腰三角形的三线合一可得出△OEC为等腰三角形,结合OE⊥AC可得出△OEC为等腰直角三角形,根据等腰直角三角形的性质可得出点C、D的坐标,由点B、D的坐标,利用待定系数法即可求出直线BD的解析式.
(1)如图1,作BF⊥AC于点F,取AB的中点G,则G(0,6),
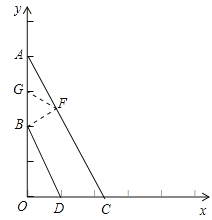
∵BD∥AC,BD与AC的距离等于2,
∴BF=2,
∵在Rt△ABF中,∠AFB=90°,AB=4,点G为AB的中点,
∴FG=BG=![]() AB=2,
AB=2,
∴△BFG是等边三角形,∠ABF=60°,
∴∠BAC=30°,
设OC=x,则AC=2x,
根据勾股定理得:OA=![]() =
=![]() x,
x,
∵OA=8,
∴x=![]() ,
,
∵点C在x轴的正半轴上,
∴点C的坐标为(![]() ,0);
,0);
(2)如图:
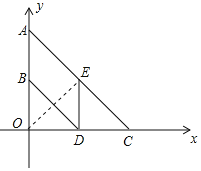
∵四边形ABDE为平行四边形,
∴DE∥AB,
∴DE⊥OC,
∵点D为OC的中点,
∴△OEC为等腰三角形,
∵OE⊥AC,
∴△OEC为等腰直角三角形,
∴∠C=45°,
∴点C的坐标为(8,0),点D的坐标为(4,0),
设直线BD的解析式为y=kx+b(k≠0),
将B(0,4)、D(4,0)代入y=kx+b,
得:![]() ,解得:
,解得:![]() ,
,
∴直线BD的解析式为y=-x+4.


科目:初中数学 来源: 题型:
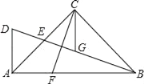
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上﹣点,连接CF,且∠ACF=∠CBG.
(1)求证:AF=CG;
(2)写出图中长度等于2DE的所有线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)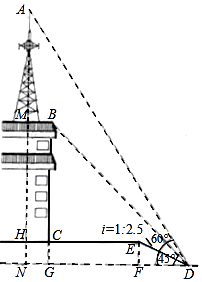
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有22名工人,每人每天可生产1200个螺钉或2000个螺母,1个螺钉需配2个螺母,为使生产的螺钉和螺母刚好配套,若设x名工人生产螺钉,依题意列方程为( )
A. 1200x=2000(22-x) B. 1200x=2![]() 2000(22-x)
2000(22-x)
C. 1200(22-x)=2000x D. 2![]() 1200x=2000(22-x)
1200x=2000(22-x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,正方形A2B2C2C1,正方形A3B3C3C2,…按如图所示的方式放置在平面直角坐标系中.点A1,A2,A3…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点Bn的坐标是__________.(n为正整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式d= ![]() 计算. 例如:求点P(﹣1,2)到直线y=3x+7的距离.
计算. 例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为d= ![]() =
= ![]() =
= ![]() .
.
根据以上材料,解答下列问题:
(1)点P(1,﹣1)到直线y=x+1的距离;
(2)已知⊙Q的圆心Q的坐标为(0,4),半径r为2,判断⊙Q与直线y= ![]() x+8的位置关系并说明理由;
x+8的位置关系并说明理由;
(3)已知直线y=﹣2x+1与y=﹣2x+6平行,A、B是直线y=﹣2x+1上的两点且AB=8,P是直线y=﹣2x+6上任意一点,求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(-3,4).
(1)求AO的长;
(2)求直线AC的解析式和点M的坐标;
(3)如图2,点P从点A出发,以每秒2个单位的速度沿折线A-B-C运动,到达点C终止.设点P的运动时间为t秒,△PMB的面积为S.
①求S与t的函数关系式;
②求S的最大值.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
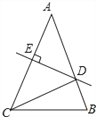
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A=40°,求∠DCB的度数;
(2)若AE=5,△DCB的周长为16,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com