
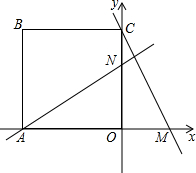
 ��ͼ�����߳�Ϊ4��������ABCO������ֱ������ϵ�У�ʹ��A��x�Ḻ�����ϣ���C��y���������ϣ���M��t��0����x���������˶�����A��ֱ��MC�Ĵ��߽�y���ڵ�N�����н��ۣ�
��ͼ�����߳�Ϊ4��������ABCO������ֱ������ϵ�У�ʹ��A��x�Ḻ�����ϣ���C��y���������ϣ���M��t��0����x���������˶�����A��ֱ��MC�Ĵ��߽�y���ڵ�N�����н��ۣ�| 2 |
| 2 |
| 2 |
| 42+42 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| k |
| x |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
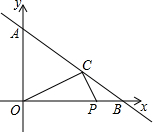 ��ͼ��ֱ��y=-
��ͼ��ֱ��y=-| 3 |
| 4 |
| A��3��m��4 | ||
| B��2��m��4 | ||
C��0��m��
| ||
| D��0��m��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ||
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
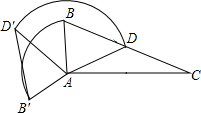 Rt��ABC�У���BAC=90�㣬BC=6����DΪBC���е㣬����ABD�Ƶ�A����ʱ�뷽����ת120��õ���AB��D�䣬���D����ת��������������·���Ƕ��٣�����������У�
Rt��ABC�У���BAC=90�㣬BC=6����DΪBC���е㣬����ABD�Ƶ�A����ʱ�뷽����ת120��õ���AB��D�䣬���D����ת��������������·���Ƕ��٣�����������У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ���ڡ�ABC�У�AB=AC��BD��AC���ϵĸߣ�����A��ֱ��L���ֱ��B��C��BE��L��CF��L��E��F�Ǵ��㣮֤����
��ͼ���ڡ�ABC�У�AB=AC��BD��AC���ϵĸߣ�����A��ֱ��L���ֱ��B��C��BE��L��CF��L��E��F�Ǵ��㣮֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3y+5 |
| 2 |
| 2y-1 |
| 3 |
| x+2 |
| 4 |
| 2x-3 |
| 6 |
| y-3 |
| -5 |
| 3y+4 |
| 15 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com