
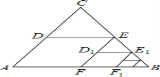
【题目】如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2017=____.
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A. 2B. 8C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年我市的脐橙喜获丰收,脐橙一上市,水果店的陈老板用2400元购进一批脐橙,很快售完;陈老板又用6000元购进第二批脐橙,所购件数是第一批的2倍,但进价比第一批每件多了20元.
(1)第一批脐橙每件进价多少元?
(2)陈老板以每件120元的价格销售第二批脐橙,售出60%后,为了尽快售完,决定打折促销,要使第二批脐橙的销售总利润不少于480元,剩余的脐橙每件售价最低打几折?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
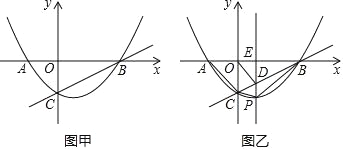
【题目】如图甲,抛物线y=ax2+bx﹣1经过A(﹣1,0),B(2,0)两点,交y轴于点C.
(1)求抛物线的表达式和直线BC的表达式.
(2)如图乙,点P为在第四象限内抛物线上的一个动点,过点P作x轴的垂线PE交直线BC于点D.
①在点P运动过程中,四边形ACPB的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
②是否存在点P使得以点O,C,D为顶点的三角形是等腰三角形?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=![]() ﹣6x+4的顶点A在直线y=kx﹣2上.
﹣6x+4的顶点A在直线y=kx﹣2上.
(1)求直线的函数表达式;
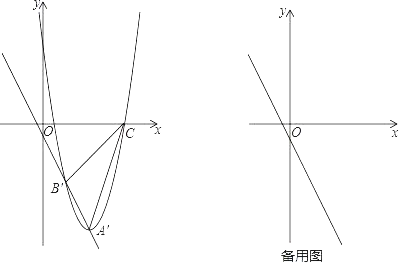
(2)现将抛物线沿该直线方向进行平移,平移后的抛物线的顶点为A′,与直线的另一交点为B′,与x轴的右交点为C(点C不与点A′重合),连接B′C、A′C.
ⅰ)如图,在平移过程中,当点B′在第四象限且△A′B′C的面积为60时,求平移的距离AA′的长;
ⅱ)在平移过程中,当△A′B′C是以A′B′为一条直角边的直角三角形时,求出所有满足条件的点A′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,

(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个倾斜角为 的斜坡,将一个小球从斜坡的坡脚 O 点处抛出,落在 A点处,小球的运动路线可以用抛物线![]() 来刻画,已知 tan
来刻画,已知 tan ![]()
(1)求抛物线表达式及点 A 的坐标.
(2)求小球在运动过程中离斜坡坡面 OA 的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
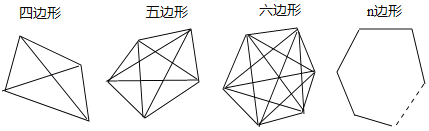
【题目】连接多边形任意两个不相邻顶点的线段称为多边形的对角线.
(1)四、五、六、n边形对角线条数分别为 、 、 、 .
(2)多边形可以有12条对角线吗?如果可以,求多边形的边数;如果不可以,请说明理由.
(3)若一个n边形的内角和为1800°,求它对角线的条数.
(4)已知k-1边形的对角线条数是![]() ,求k+1边形的对角线条数(k>4).
,求k+1边形的对角线条数(k>4).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日,武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是![]() .”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
.”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com