
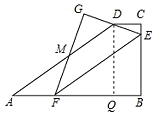
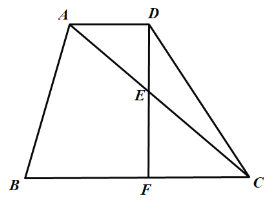
【题目】在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() 为
为![]() 上一点,过点
上一点,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() .将
.将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,当
,当![]() 过点
过点![]() 时,
时,![]() 的长为__________.
的长为__________.

【答案】![]()
【解析】
根据平行线的性质得到∠A=∠EFB,∠GFE=∠AMF,根据轴对称的性质得到∠GFE=∠BFE,求得∠A=∠AMF,得到AF=FM,作DQ⊥AB于点Q,求得∠AQD=∠DQB=90 ![]() .根据矩形的性质得到CD=QB=2,QD=CB=6,求得AQ=102=8,根据勾股定理得到AD=
.根据矩形的性质得到CD=QB=2,QD=CB=6,求得AQ=102=8,根据勾股定理得到AD=![]() =10,设EB=3x,求得FB=4x,CE=63x,求得AF=MF=104x,GM=8x10,根据相似三角形的性质得到GD=6x
=10,设EB=3x,求得FB=4x,CE=63x,求得AF=MF=104x,GM=8x10,根据相似三角形的性质得到GD=6x![]() ,求得DE=
,求得DE=![]() 3x,根据勾股定理列方程即可得到结论.
3x,根据勾股定理列方程即可得到结论.
如图,∵EF∥AD,
∴∠A=∠EFB,∠GFE=∠AMF,
∵△GFE与△BFE关于EF对称,
∴△GFE≌△BFE,
∴∠GFE=∠BFE,
∴∠A=∠AMF,
∴△AMF是等腰三角形,
∴AF=FM,
作DQ⊥AB于点Q,
∴∠AQD=∠DQB=90![]() .
.
∵AB∥DC,
∴∠CDQ=90![]() .
.
∵∠B=90![]() ,
,
∴四边形CDQB是矩形,
∴CD=QB=2,QD=CB=6,
∴AQ=102=8,
在Rt△ADQ中,由勾股定理得
AD=![]() =10,
=10,
∵tanA=![]() ,
,
∴tan∠EFB=![]() ,
,
设EB=3x,
∴FB=4x,CE=63x,
∴AF=MF=104x,
∴GM=8x10,
∵∠G=∠B=∠DQA=90°,∠GMD=∠A,
∴△DGM∽△DQA,
∴![]() ,
,
∴GD=6x![]() ,
,
∴DE=![]() 3x,
3x,
在Rt△CED中,由勾股定理得
(![]() 3x)2(63x)2=4,
3x)2(63x)2=4,
解得:3x=![]() ,
,
∴当EG过点D时BE=![]() .
.
故答案为:![]() .
.


 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
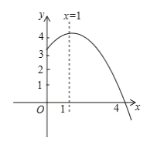
【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
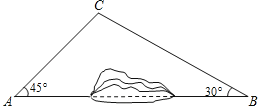
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶,已知BC=80千米,∠A=45°,∠B=30°,
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到1千米)(参考数据:![]() =1.4,
=1.4,![]() =1.7)
=1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
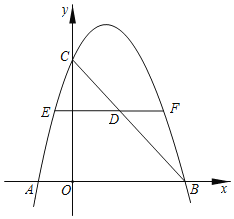
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
(1)求抛物线的对称轴和函数表达式.
(2)连结BC线段,BC上有一点D,过点D作x轴的平行线交抛物线于点E,F,若EF=6,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
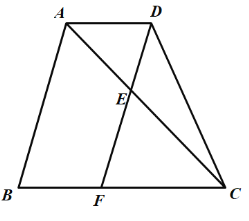
【题目】已知:在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在对角线
在对角线![]() 上(不与点
上(不与点![]() 重合),
重合),![]() ,
,![]() 的延长线与射线
的延长线与射线![]() 交于点
交于点![]() ,设
,设![]() 的长为
的长为![]() .
.
(1)如图,当![]() 时,求
时,求![]() 的长;
的长;
(2)设![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并直接写出定义域;
的函数解析式,并直接写出定义域;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
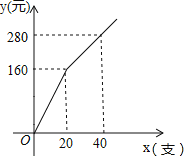
【题目】某校九年级决定购买学习用具对在本次适应性考以中成绩突出的同学进行奖励,其中计划购买,A、B两种型号的钢笔共45支,已知A种钢笔的单价为7元/支,购买B种钢笔所需费用y(元)与购买数量x(支)之间存在如图所示的函数关系式.
(1)求y与x的函数关系式;
(2)若购买计划中,B种钢笔的数最不超过35支,但不少于A种钢笔的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=40°,连接BD、CE.将△ADE绕点A旋转,BD、CE也随之运动.

(1)求证:BD=CE;
(2)在△ADE绕点A旋转过程中,当AE∥BC时,求∠DAC的度数;
(3)如图②,当点D恰好是△ABC的外心时,连接DC,判断四边形ADCE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
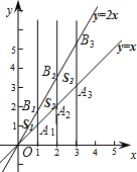
【题目】 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…,四边形An-1AnBnBn-1的面积记作Sn,那么S2019=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com