
科目:初中数学 来源: 题型:
在平面直角坐标系xOy中,一次函数 的图象与反比例函数
的图象与反比例函数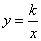 的图象的一
的图象的一
个交点为A(1,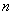 ).
).
(1)求反比例函数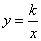 的解析式;
的解析式;
(2)若P是坐标轴上一点(P不与O重合),且满足 ,直接写出点P的坐标.
,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
问题提出
平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一
直线上),能否在同一个圆呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
⑴当C、D在线段AB的同侧时,
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 ;
如图②,若点D在⊙O内,此时有∠ACB ∠ADB;
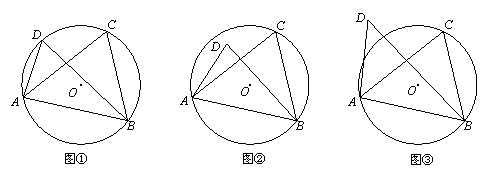 如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);
如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.
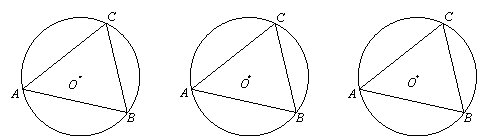 |
此时有 , 此时有 , 此时有 .
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
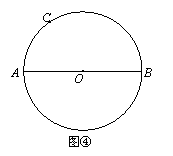 (3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图,AB是⊙O的直径,点C在⊙O上.
求作:CN⊥AB.
作法:①连接CA,CB;
②在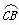 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
有一组对角都是直角,且另一组对角不相等的四边形叫做准矩形.下列叙述:①直角梯形是准矩形;②准矩形中,夹一个直角的两边的平方和等于夹另一个直角的两边的平方和;③准矩形中,以两个直角顶点为端点的对角线的长小于另一条对角线的长.其中,所有正确叙述的序号是
A.①②③ B.② C.③ D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
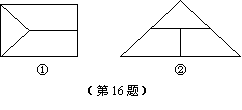
将一个相邻两边长分别为m、n的矩形按图①的方式分割成两个全等的梯形和一个小三角形,如果这两个梯形和小三角形能按图②的方式无缝隙、不重叠的拼成大三角形,那么m、n之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
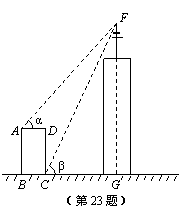 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点处测得该塔顶端F的仰角分别为∠α=48°,∠β=65°,矩形建筑物宽度AD=20 m,高度DC=33 m.计算该信号发射塔顶端到地面的高度FG(结果精确到1m).(参考数据:sin48°≈0.7,cos48°≈0.7,tan48°≈1.1,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)
如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点处测得该塔顶端F的仰角分别为∠α=48°,∠β=65°,矩形建筑物宽度AD=20 m,高度DC=33 m.计算该信号发射塔顶端到地面的高度FG(结果精确到1m).(参考数据:sin48°≈0.7,cos48°≈0.7,tan48°≈1.1,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知下列命题:①对角线互相垂直平分且相等的四边形是正方形;
②反比例函数y=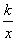 ,当k>0时,y随x的增大而减少;
,当k>0时,y随x的增大而减少;
③在一个圆中,如果弦相等,那么所对的圆周角相等,其中真命题为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
在篮球比赛中,某队员连续10场比赛中每场的得分情况如下表所示:
| 场次(场) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分(分) | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 38 |
则这10场比赛中他得分的中位数和众数分别是( )
A.10,4 B.10,7 C.7,13 D.13,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com