
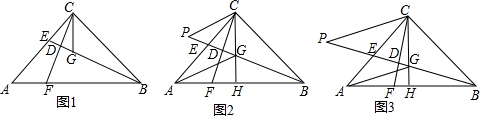
 已知:如图,D、E分别是△ABC两边AB、AC上的点,试问在下列条件下△ADE与△ACB是否相似,并说明理由.
已知:如图,D、E分别是△ABC两边AB、AC上的点,试问在下列条件下△ADE与△ACB是否相似,并说明理由.分析 (1)两角对应相等,两三角形相似;
(2)根据内角和求∠B=50°,根据两角对应相等,两三角形相似;
(3)根据两边的比相等,且夹角相等,则两三角形相似.
解答 解:(1)∵∠AED=∠B,∠A=∠A,
∴△AED∽△ABC;
(2)∵∠A=60°,∠C=70°,
∴∠B=180°-60°-70°=50°,
∵∠AED=50°,
∴∠B=∠AED,
∵∠A=∠A,
∴△AED∽△ABC;
(3)∵AD=3,BD=5,AE=4,EC=2,
∴$\frac{AD}{AC}$=$\frac{3}{4+2}$=$\frac{1}{2}$,$\frac{AE}{AB}$=$\frac{4}{3+4}$=$\frac{1}{2}$,
∴$\frac{AD}{AC}=\frac{AE}{AB}$,
∵∠A=∠A,
∴∴△AED∽△ABC.
点评 本题考查了三角形相似的判定,熟练掌握三角形相似的判定方法是关键,要注意:公共角或对顶角.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
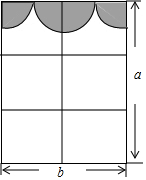 某房间窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同):
某房间窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
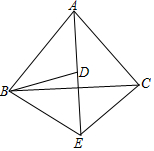 如图所示,已知$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$.∠ABD=20°,求∠EBC的大小.
如图所示,已知$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$.∠ABD=20°,求∠EBC的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com