
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 坐标为(-3,2),点
坐标为(-3,2),点![]() 坐标为(n,-3).
坐标为(n,-3).
(1)求一次函数和反比例函数的表达式;
(2)如果点![]() 是
是![]() 轴上一点,且
轴上一点,且![]() 的面积是5,求点
的面积是5,求点![]() 的坐标.
的坐标.
(3)利用函数图象直接写出关于x的不等式![]() 的解集.
的解集.

【答案】(1)一次函数表达式为y=-x-1;反比例函数表达式为y=-![]() ;(2)点P的坐标是(-3,0)或(1,0);(3)-3<x<0或x>0
;(2)点P的坐标是(-3,0)或(1,0);(3)-3<x<0或x>0
【解析】
(1)将A坐标代入双曲线解析式中求出m的值,确定出双曲线的解析式,再将A与B坐标代入一次函数解析式中求出k与b的值,即可确定出一次函数解析式;
(2)求得直线与x轴的交点是(-1,0),设点P的坐标是(a,0),则![]() 的底为|a+1|,利用三角形面积公式即可求得点P的坐标;
的底为|a+1|,利用三角形面积公式即可求得点P的坐标;
(3)根据一次函数与反比例函数的两交点A与B的横坐标以及0,将x轴分为四个范围,找出反比例图象在一次函数图象上方时x的范围即可.
(1)∵双曲线![]() (m≠0)过点A(-3,2),
(m≠0)过点A(-3,2),
∴m=-3×2=-6,
∴反比例函数表达式为![]() .
.
∵点B(n,-3)在反比例函数![]() 的图象上,
的图象上,
∴n=2,B(2,-3).

∵点A(-3,2)与点B(2,-3)在直线y=kx+b上,
∴![]() 解得
解得![]()
∴一次函数表达式为y=-x-1;
(2)如解图,在x轴上任取一点P,连接AP,BP,由(1)知点B的坐标是(2,-3).
在y=-x-1中令y=0,解得x=-1,则直线与x轴的交点是(-1,0).
设点P的坐标是(a,0).
∵△ABP的面积是5,
∴![]() ·|a+1|·(2+3)=5,
·|a+1|·(2+3)=5,
则|a+1|=2,
解得a=-3或1.
则点P的坐标是(-3,0)或(1,0).
(3) 根据图象得: -3<x<0或x>0


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)2018年,绿云花市的张老板一共销售![]() 两个品种的绿色植物共900盆. 其中
两个品种的绿色植物共900盆. 其中![]() 品种每盆20元,
品种每盆20元,![]() 品种每盆30元,从销售额为23000元,请求出销售的
品种每盆30元,从销售额为23000元,请求出销售的![]() 品种绿色植物的数量;
品种绿色植物的数量;
(2)2019年,![]() 品种绿色植物比上一年的价格优惠
品种绿色植物比上一年的价格优惠![]() ,
,![]() 品种绿色植物比上一年的价格优惠
品种绿色植物比上一年的价格优惠![]() .
.
由于市民对绿色植物的需求量持续增加,张老板售出的![]() 品种绿色植物比上一年的数量增加了
品种绿色植物比上一年的数量增加了![]() ,售出的
,售出的![]() 品种绿色植物比上一年的数量增加了
品种绿色植物比上一年的数量增加了![]() ,总销售额比上一年增加了
,总销售额比上一年增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3经过点A(﹣1,0),B(3,0),与y轴交于点C.点D(xD,yD)为抛物线上一个动点,其中1<xD<3.连接AC,BC,DB,DC.
(1)求该抛物线的解析式;
(2)当△BCD的面积等于△AOC的面积的2倍时,求点D的坐标;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
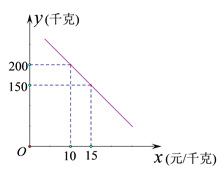
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间的函数关系如图所示.
(元/千克)之间的函数关系如图所示.
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在圆O上,BE⊥CD垂足为E,CB平分∠ABE,连接BC
(1)求证:CD为⊙O的切线;
(2)若cos∠CAB=![]() ,CE=
,CE=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“阳光体育”活动时间,甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定甲打第一场,再从其余三位同学中随机选取一位,恰好选中丙同学的概率为 ;
(2)用画树状图或列表的方法,求恰好选中甲、乙两位同学进行比赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com