
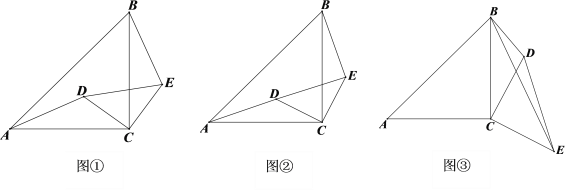
【题目】如图①已知△ACB和△DCE为等腰直角三角形,按如图的位置摆放,直角顶点
C重合.
(1)求证:AD=BE;
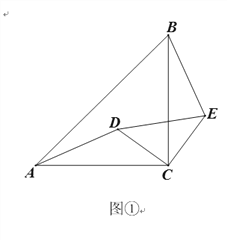
(2)将△DCE绕点C旋转得到图②,点A、D、E在同一直线上时,若CD=![]() ,BE=3,
,BE=3,
求AB 的长;
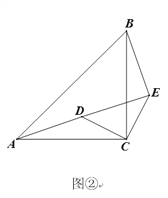
(3)将△DCE绕点C顺时针旋转得到图③,若∠CBD=45°,AC=6,BD=3,求BE的长.
【答案】(1)证明见解析;(2)![]() ;(3)9
;(3)9
【解析】(1)利用等腰直角三角形的性质求出∠ACD=∠ECB,用SAS证明△ACD≌△BCE即可;(2)利用(1)的结论∠AEB=90°,在Rt△AEB中,用勾股定理求出AB;(3)连接AD, 求出∠ABD=90°,在Rt△ADB中,用勾股定理求出AD,由△ACD≌△BCE即可求得BE.
解:(1)∵△ACB和△DCE为等腰直角三角形
∴AC=CB,DC=CE,
∠ACB=90°, ∠DCE=90°
∴∠ACB-∠DCB =∠DCE-∠DCB
即∠ACD=∠ECB
∴△ACD≌△BCE (SAS)
∴AD=BE
(2)解:
∵△DCE为等腰直角三角形
∴DC=EC=![]()
∴DE=2
∵△ACD≌△BCE (SAS)
∴AD=BE=3
∠ADC=∠BEC=180°-45°=135°
∴∠AEB=135°-45°=90°
在Rt △AEB中,AB=![]()
(3)连接AD,
∵△ACB为等腰直角三角形
∴AC=BC=6, ∠ABC=45°
∴AB=![]()
∵∠CBD=45°
∴∠ABD=45°+45°=90°
在Rt △ADB中,AD=![]()
∵△ACD≌△BCE (SAS)
∴AD=BE=9
“点睛”本题考查了等腰直角三角形的性质、全等三角形及勾股定理的运用,解题关键是证明两个三角形全等,解题时要考虑辅助线的作法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某种植物的主干长出若干数目的支干,每个支干又长出相同数目的小分支,若小分支、支干和主干的总数目是73,则每个支干长出的小分支的数目为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目 (被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
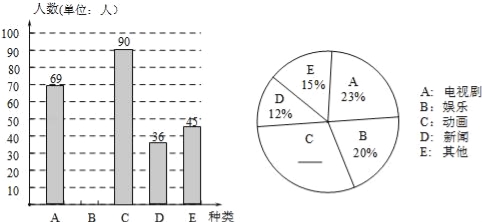
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,解答后面提出的问题:
黑白双雄,纵横江湖;双剑合壁,天下无敌,这是武侠小说中的常见描述,其意思是指两个人合在一起,取长补短,威力无比,在二次根式中也有这种相辅相成的“对子”,如:(2+![]() )(2-
)(2-![]() )=1,(
)=1,(![]() +
+![]() )(
)(![]() -
-![]() )=3, 它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
)=3, 它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:![]() =
=![]() =
=![]() ,
,![]() =
=![]() =7+4
=7+4![]() .像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
.像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
解决问题:
(1)4+![]() 的有理化因式是 ,将
的有理化因式是 ,将![]() 分母有理化得 ;
分母有理化得 ;
(2)已知x=![]() ,y=
,y=![]() ,则
,则![]() = ;
= ;
(3)已知实数x,y满足(x+![]() )(y+
)(y+![]() )-2017=0,则x= ,y= .
)-2017=0,则x= ,y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
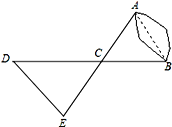
【题目】如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在DB的中点C处有一个雕塑,小川从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A、B两点之间的距离.
(1)你能说明小川这样做的根据吗?
(2)如果小川恰好未带测量工具,但是知道A和假山D、雕塑C分别相距200米、120米,你能帮助他确定AB的长度范围吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com