
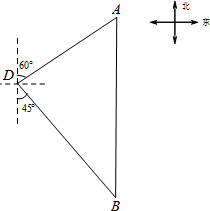
 ���㵺�Թ����������й�����ʥ������Ϊ������Ȩ���Һ��ബ��ӷ����ڵ��㵺�����������άȨ�����ͼ��һ�Һ��ബλ�ڵ��㵺D�ı�ƫ��60�㷽������㵺�ľ���Ϊ16�����A�����������Ϸ����У�����1Сʱ���ִ�ʱ���ബλ�ڵ��㵺����ƫ��45�㷽���ϵ�B����
���㵺�Թ����������й�����ʥ������Ϊ������Ȩ���Һ��ബ��ӷ����ڵ��㵺�����������άȨ�����ͼ��һ�Һ��ബλ�ڵ��㵺D�ı�ƫ��60�㷽������㵺�ľ���Ϊ16�����A�����������Ϸ����У�����1Сʱ���ִ�ʱ���ബλ�ڵ��㵺����ƫ��45�㷽���ϵ�B�������� ��1������D��DC��AB������Rt��ADC����DC�ij�������ֱ�ǡ�BDC�����DB��
��2������ֱ����������30�����Եıߵ���б�ߵ�һ�����AC�������õ���ֱ�������ε�֪ʶ���BC�ij������ɵó�AB�ij���Ȼ�������ٶ�=·�̡�ʱ����м������ٶȣ�
���  �⣺��1����DC��AB��C�㣬
�⣺��1����DC��AB��C�㣬
���ADC=30�㣬��BDC=45�� AD=16�������
��Rt��ADC��cos��ADC=$\frac{DC}{DA}$��
��DC=AD•cos��ADC=8$\sqrt{3}$�������
��Rt��DCB��cos��BDC=$\frac{DC}{DB}$��
��DB=$\frac{DC}{cos��BDC}$=$\frac{8\sqrt{3}}{cos45��}$=8$\sqrt{6}$�������
�𣺴�ʱ���ബ���ڵ�B������㵺�ľ�����8$\sqrt{6}$���
��2����DA=16�����ADC=30�㣬��ACD=90�㣬
��AC=8���
�ߡ�CDB=45�㣬��ACD=90�㣬
���CBD=45�㣬
��DC=BC=8$\sqrt{3}$���
��AB=AC+BC=8+8$\sqrt{3}$�������
�����Һ��ബ���ٶ��ǣ���8+8$\sqrt{3}$����1=8+8$\sqrt{3}$��30������/ʱ��
�����Һ��ബ���ٶ�ԼΪ30����/ʱ��
���� ������Ҫ�����˽�ֱ�������ε�Ӧ��-��������⣬�������εı�ߵ�����һ�����ת��Ϊ��ֱ�������ε����⣬����ķ������������ߣ�


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
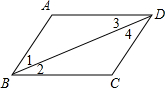 ����ͼ�У��������ж�AD��BC�ǣ�������
����ͼ�У��������ж�AD��BC�ǣ�������| A�� | ��1=��2 | B�� | ��3=��4 | C�� | ��2=��3 | D�� | ��1=��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
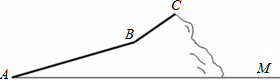 ��ѧ�С����֯һ�ε�ɽ������Ǵ�ɽ����A�������б��AB����B�㣬�ٴ�B����б��BC����ɽ��C�㣬·����ͼ��ʾ��б��AB�ij�Ϊ200$\sqrt{13}$�ף�б��BC�ij�Ϊ200$\sqrt{2}$�ף��¶���1��1����֪A�㺣��121�ף�C�㺣��721�ף�
��ѧ�С����֯һ�ε�ɽ������Ǵ�ɽ����A�������б��AB����B�㣬�ٴ�B����б��BC����ɽ��C�㣬·����ͼ��ʾ��б��AB�ij�Ϊ200$\sqrt{13}$�ף�б��BC�ij�Ϊ200$\sqrt{2}$�ף��¶���1��1����֪A�㺣��121�ף�C�㺣��721�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | 2 | C�� | 3$\sqrt{2}$ | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3 | B�� | 3 | C�� | -3 | D�� | ���ϴ𰸶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
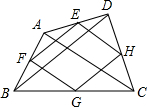 ��ͼ�������ı���ABCD�����е㣬�õ��ı���EFGH��ֻҪ����AC=BD���������ܱ�֤�ı���EFGH�����Σ�
��ͼ�������ı���ABCD�����е㣬�õ��ı���EFGH��ֻҪ����AC=BD���������ܱ�֤�ı���EFGH�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
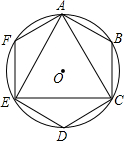 �ڵȱߡ�ACE�ڽ��ڡ�O������B��D��F�ֱ���$\widehat{AB}$��$\widehat{CE}$��$\widehat{AE}$���е㣬����AB��BC��CD��DE��EF��FA������ͼ���Ƶ�O��תһ�����ʵĽǶȺ����ԭͼ���غϣ��������ת�ǵĶ��������ǣ�������
�ڵȱߡ�ACE�ڽ��ڡ�O������B��D��F�ֱ���$\widehat{AB}$��$\widehat{CE}$��$\widehat{AE}$���е㣬����AB��BC��CD��DE��EF��FA������ͼ���Ƶ�O��תһ�����ʵĽǶȺ����ԭͼ���غϣ��������ת�ǵĶ��������ǣ�������| A�� | 60�� | B�� | 90�� | C�� | 120�� | D�� | 180�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com