
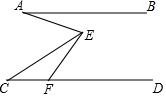
 如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为36°或37°.
如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为36°或37°. 分析 先过E作EG∥AB,根据平行线的性质可得∠AEF=∠BAE+∠DFE,再设∠CEF=x,则∠AEC=2x,根据6°<∠BAE<15°,即可得到6°<3x-60°<15°,解得22°<x<25°,进而得到∠C的度数.
解答 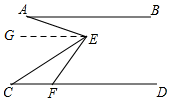 解:如图,过E作EG∥AB,
解:如图,过E作EG∥AB,
∵AB∥CD,
∴GE∥CD,
∴∠BAE=∠AEG,∠DFE=∠GEF,
∴∠AEF=∠BAE+∠DFE,
设∠CEF=x,则∠AEC=2x,
∴x+2x=∠BAE+60°,
∴∠BAE=3x-60°,
又∵6°<∠BAE<15°,
∴6°<3x-60°<15°,
解得22°<x<25°,
又∵∠DFE是△CEF的外角,∠C的度数为整数,
∴∠C=60°-23°=37°或∠C=60°-24°=36°,
故答案为:36°或37°.
点评 本题主要考查了平行线的性质以及三角形外角性质的运用,解决问题的关键是作平行线,解题时注意:两直线平行,内错角相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 众数是10.5 | B. | 中位数是10 | C. | 平均数是11 | D. | 以上说法均不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是我国古代某种铜钱的平面示意图,该图形是在一个圆形的中间挖去一个正方形得到的.若圆的半径是3cm,正方形的边长为xcm,设该图形的面积为ycm2.(注:π取3)
如图是我国古代某种铜钱的平面示意图,该图形是在一个圆形的中间挖去一个正方形得到的.若圆的半径是3cm,正方形的边长为xcm,设该图形的面积为ycm2.(注:π取3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<-2 | B. | x<-4 | C. | -4<x<-2 | D. | 无解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com