
分析 (1)设该公司生产每件商品的成本为a元,根据:实际售价-成本=利润,列出方程,解方程可得;
(2)根据:每天利润=单件利润×每天销售量列出函数关系式,配方成顶点式可得函数的最值情况;
(3)根据(2)中每天利润减去每天开支a元列出函数关系式P=-4(x-25)2+2500-a,根据每天的最大利润不低于2200元可得关于a的不等式,解不等式可得a的取值范围,再由至少有46天盈利可知-4x2+200x-a=0的两根x1、x2间距离x1-x2≥46,根据韦达定理可得关于a的不等式,求得a的范围,综合上述情况确定a的范围..
解答 解:(1)设该公司生产每件商品的成本为a元,根据题意,
得:0.8×(10+20)-a=0.2a,
解得:a=20,
故该公司生产每件商品的成本为20元;
(2)设第x天的销售利润为W,
则:W=(x+20-20)(-4x+200)=-4x2+200x=-4(x-25)2+2500,
∴当x=25时,W取得最大值,最大值为2500元,
故问销售该商品第25天时,每天的利润最大,最大利润是2500元;
(3)记公司每天控制人工、水电和房租支出共计a元后利润为P,
则P=-4(x-25)2+2500-a,
根据题意:2500-a≥2200,
解得:a≤300,
又∵至少有46天的盈利,
∴-4x2+200x-a=0的两根x1、x2间距离x1-x2≥46,
∴(x1-x2)2≥462,即(x1+x2)2-4x1x2≥462,
∵x1+x2=50,x1x2=$\frac{a}{4}$,
∴502-4×$\frac{a}{4}$≥462,解得:a≤384,
综上,0<a≤300,
故答案为:0<a≤300.
点评 本题主要考查二次函数的实际应用能力,明确不等关系并据此列出方程或函数关系式是解题基础,根据题意挖掘出不等关系求a的范围是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
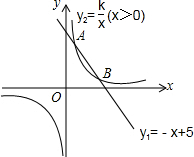 如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n).
如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
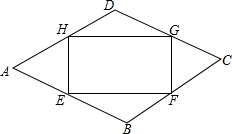 如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH.其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°
如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH.其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
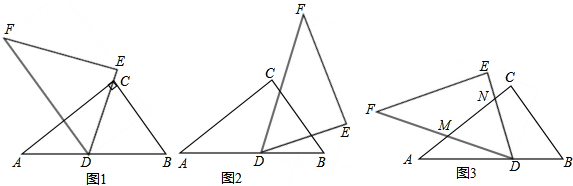
 将抛物线c1:$y=-\sqrt{3}{x^2}+\sqrt{3}$沿x轴翻折,得到抛物线c2,如图1所示.
将抛物线c1:$y=-\sqrt{3}{x^2}+\sqrt{3}$沿x轴翻折,得到抛物线c2,如图1所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com