
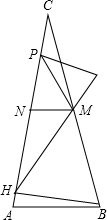
 如图,△ABC中,M,N分别是BC,AC的中点,BH是AC边上的高线,∠HMN=45°,MP垂直∠HMN的平分线并交AC于点P,若PH=$\frac{1}{2}$(AB+BC),求证:△ABC是等腰三角形.
如图,△ABC中,M,N分别是BC,AC的中点,BH是AC边上的高线,∠HMN=45°,MP垂直∠HMN的平分线并交AC于点P,若PH=$\frac{1}{2}$(AB+BC),求证:△ABC是等腰三角形. 分析 作辅助线,在Rt△BHC中,根据直角三角形斜边上的中线得:MH=$\frac{1}{2}$BC,由中位线定理得:MN=$\frac{1}{2}$AB,MN∥AB,根据PH=$\frac{1}{2}$(AB+BC)可得:PH=HK,则△PHK是等腰三角形,再证明△PMN≌△PMK(SAS),得∠CNM=∠K,设∠CHM=α,
分别表示出∠A和∠ABC的度数,发现都等于90°-$\frac{1}{2}$α,则∠A=∠ABC,所以△ABC是等腰三角形.
解答 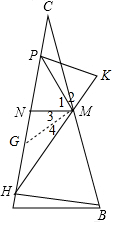 证明:延长HM至点K,使得MN=MK,作∠NMH的交平分线交AC于点G,连接PK,
证明:延长HM至点K,使得MN=MK,作∠NMH的交平分线交AC于点G,连接PK,
∵BH⊥AC,M是BC的中点,
∴MH=$\frac{1}{2}$BC,
∵M、N分别是BC、AC的中点,
∴MN=$\frac{1}{2}$AB,MN∥AB,
∵PH=$\frac{1}{2}$(AB+BC),
∴PH=$\frac{1}{2}$AB+$\frac{1}{2}$BC=MN+MH=MK+MH=KH,
∵MG平分∠NMH,∠NMH=45°,
∴∠3=∠4=22.5°,
∵PM⊥MG,
∴∠1=∠2=67.5°,
在△PMN和△PMK中,
∵$\left\{\begin{array}{l}{MN=MK}\\{∠1=∠2}\\{PM=PM}\end{array}\right.$,
∴△PMN≌△PMK(SAS),
∴∠CNM=∠K,
设∠CHM=α,
∵HK=HP,
∴∠K=∠HPK=$\frac{180°-α}{2}$=90°-$\frac{1}{2}$α,
则∠CNM=∠K=90°-$\frac{α}{2}$,
∵MN∥AB,
∴∠A=∠CNM=90°-$\frac{1}{2}$α,
∴∠ABC=180°-∠C-∠A=180°-α-90°+$\frac{1}{2}$α=90°-$\frac{1}{2}$α,
∴∠A=∠ABC,
∴△ABC是等腰三角形.
点评 本题考查了三角形的中位线定理、等腰三角形的性质与判定及直角三角形斜边中线的性质,比较复杂,难度较大,熟练掌握这此定理及性质是解题的关键,本题从直角三角形斜边中点为突破口,利用了直角三角形斜边中线的性质得出边相等,从而得出角的关系,设未知数,将所要求的∠A和∠ABC的度数表示出来,得出相等关系,利用等腰三角形的判定得出结论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,一次函数y=kx+3的图象与反比例函数y=$\frac{m}{x}$的图象在第四象限交于点P.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、点D,且S△DBP=27,$\frac{OC}{CA}$=$\frac{1}{2}$.
已知:如图,一次函数y=kx+3的图象与反比例函数y=$\frac{m}{x}$的图象在第四象限交于点P.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、点D,且S△DBP=27,$\frac{OC}{CA}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com