
| A. | b是a、c的比例中项,且a:b=7:3,则b:c=7:3 | |
| B. | 正三角形、菱形、矩形中,对称轴最多的是菱形 | |
| C. | 如果点C是线段的黄金分割点,那么AC=0.618AB | |
| D. | 相似图形一定是位似图形 |
分析 分别根据比例的性质、轴对称的性质、黄金分割点的定义及位似图形的定义对各选项进行逐一分析即可.
解答 解:A、∵b是a、c的比例中项,且a:b=7:3,∴$\frac{a}{b}$=$\frac{b}{c}$,∴b:c=7:3,故本选项正确;
B、∵正三角形有三条对称轴、菱形是中心对称图形、矩形由两条对称轴,所以对称轴最多的是正三角形,故本选项错误;
C、如果点C是线段的黄金分割点,只有当AC>BC时,AC≈0.618AB,故本选项错误;
D、相似图形不一定是位似图形,故本选项错误.
故选A.
点评 本题考查的是命题与定理,熟知比例的性质、轴对称的性质、黄金分割点的定义及位似图形的定义是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
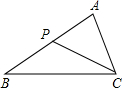 如图,点P是△ABC的边AB上的一点,下列条件中不能得到△ACP∽△ABC的是( )
如图,点P是△ABC的边AB上的一点,下列条件中不能得到△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AP}{AC}=\frac{AC}{AB}$ | D. | $\frac{AP}{AC}=\frac{PC}{CB}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com