
分析 (1)只要证明△BAD≌△CAE,CE=BD,∠ACE=∠B,得到∠BCE=∠BCA+∠ACE=90°,于是有CE=BD,CE⊥BD.
(2)结论不变.证明的方法与(1)一样.
(3)①当锐角∠ACB=45°时,CE⊥BD.过A作AM⊥BC于M,EN⊥AM于N,根据旋转的性质得到∠DAE=90°,AD=AE,利用等角的余角相等得到∠NAE=∠ADM,易证得Rt△AMD≌Rt△ENA,则NE=MA,由于∠ACB=45°,则AM=MC,所以MC=NE,易得四边形MCEN为矩形,得到∠DCF=90°,
②由Rt△AMD∽Rt△DCF,得$\frac{MD}{CF}$=$\frac{AM}{DC}$,由此构建二次函数,再利用二次函数即可求得CF的最大值.
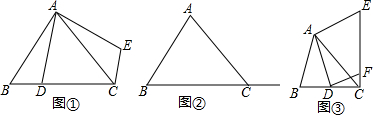
解答 解:(1)CE=BD,CE⊥BD;
理由:如图①中,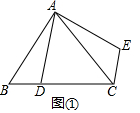
∵AB=AC,∠BAC=90°,
∴线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∠BAD=∠CAE,
∴△BAD≌△CAE,
∴CE=BD,∠ACE=∠B,
∴∠BCE=∠BCA+∠ACE=90°,
∴线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD;
(2)结论:(1)中的结论仍然成立.理由如下:
如图②中,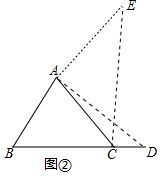
∵线段AD绕点A逆时针旋转90°得到AE,
∴AE=AD,∠DAE=90°,
∵AB=AC,∠BAC=90°
∴∠CAE=∠BAD,
∴△ACE≌△ABD,
∴CE=BD,∠ACE=∠B,
∴∠BCE=90°,
所以线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD;
(3)①结论:当锐角∠ACB=45°时,CE⊥BD.理由如下:
如图③中,过A作AM⊥BC于M,EN⊥AM于N,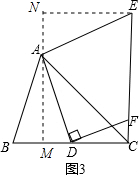
∵线段AD绕点A逆时针旋转90°得到AE,
∴∠DAE=90°,AD=AE,
∴∠NAE=∠ADM,
易证得Rt△AMD≌Rt△ENA,
∴NE=AM,
∵∠ACB=45°,
∴△AMC为等腰直角三角形,
∴AM=MC,
∴MC=NE,
∵AM⊥BC,EN⊥AM,
∴NE∥MC,
∴四边形MCEN为平行四边形,
∵∠AMC=90°,
∴四边形MCEN为矩形,
∴∠DCF=90°,
∴EC⊥BD.
②∵Rt△AMD∽Rt△DCF,
∴$\frac{MD}{CF}$=$\frac{AM}{DC}$,
设DC=x,
∵∠ACB=45°,AC=3 $\sqrt{2}$,
∴AM=CM=3,MD=3-x,
∴$\frac{3-x}{CF}$=$\frac{3}{x}$,
∴CF=-$\frac{1}{3}$x2+x=-$\frac{1}{3}$(x-$\frac{3}{2}$)2+$\frac{3}{4}$,
∵-$\frac{1}{3}$<0,
∴当x=1.5时,CF有最大值,最大值为$\frac{3}{4}$.
故答案为45,$\frac{3}{4}$;
点评 本题考查三角形综合题、旋转变换、等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定与性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形或全等三角形解决问题,学会构建二次函数解决最值问题,属于中考压轴题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
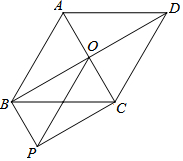 如图,在菱形ABCD中,AC、BD交于点O,BP∥AC,CP∥BD.
如图,在菱形ABCD中,AC、BD交于点O,BP∥AC,CP∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
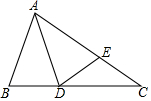 如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,E为AC上一点,AE=AB,连接DE.
如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,E为AC上一点,AE=AB,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运往地 车型 | 甲地(元/辆) | 乙地(元/辆) |
| 大货车 | 720 | 800 |
| 小货车 | 500 | 650 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
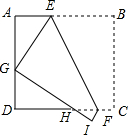 如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE=4$\sqrt{3}$-2时,△EGH为等腰三角形.
如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE=4$\sqrt{3}$-2时,△EGH为等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
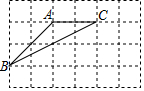 如图,将△ABC放在每个小正方形的边长为l的网格中,点A,B,C均落在格点上.
如图,将△ABC放在每个小正方形的边长为l的网格中,点A,B,C均落在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com