
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= ![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= ![]() BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB= ![]() BC,
BC,
∴AE= ![]() BC,
BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴SABCD=ABAC,故②正确,
∵AB= ![]() BC,OB=
BC,OB= ![]() BD,
BD,
∵BD>BC,
∴AB≠OB,故③错误;
∵CE=BE,CO=OA,
∴OE= ![]() AB,
AB,
∴OE= ![]() BC,故④正确.
BC,故④正确.
故C符合题意.
故答案为:C.
解答此题的关键是掌握平行四边形的性质和证得△ABE是等边三角形.在平行四边形的性质易得△ABE是等边三角形,又由![]() ,证得①;继而证得AC⊥AB,得到②;可得OE是△ABC的中位线,从而得到
,证得①;继而证得AC⊥AB,得到②;可得OE是△ABC的中位线,从而得到![]() ,可证得④.由
,可证得④.由![]() ,
,![]() ,BD>BC,可得AB≠OB可得③错误.
,BD>BC,可得AB≠OB可得③错误.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F,下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有( )

A. 4个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( ) 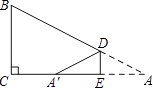
A.![]()
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上: .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别![]() a、
a、![]() a、
a、![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y= ![]() (x>0)的图象与边BC交与点F.
(x>0)的图象与边BC交与点F.
(1)若△OAE、△OCF的面积分别为S1、S2 , 且S1+S2=2,求k的值;
(2)在(1)的结论下,当OA=2,OC=4时,求三角形OEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )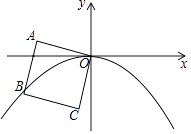
A.![]()
B.![]()
C.﹣2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
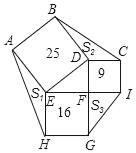
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com