

分析 (1)利用待定系数法求出直线AB的函数解析式;
(2)先证出△BDO≌△COD,得出∠BDO=∠CDO,再根据∠CDO=∠ADP,即可得出∠BDE=∠ADP,再连结PE,根据∠ADP=∠DEP+∠DPE,∠BDE=∠ABD+∠OAB,∠ADP=∠BDE,∠DEP=∠ABD,得出∠DPE=∠OAB,再证出∠DFE=∠DPE=45°,最后根据∠DEF=90°,得出△DEF是等腰直角三角形,得到答案;
(3)BD:BF=2:1时,过点F作FH⊥OB于点H,证出△BOD∽△FHB,再根据∠FHO=∠EOH=∠OEF=90°,得出四边形OEFH是矩形,OE=FH=2,EF=OH=4OD,根据DE=EF,求出OD的长,从而得出直线CD的解析式,最后根求出点P的坐标即可;连结EB,先证出△DEF是等腰直角三角形,过点F作FG⊥OB于点G,同理可得△BOD∽△FGB,得出FG,ODBG,再证出四边形OEFG是矩形,求出OD的值,再求出直线CD的解析式,最后根即可求出点P的坐标.
解答 解:(1)设直线AB的函数解析式为:y=kx+b,
由题意得,$\left\{\begin{array}{l}{b=2}\\{2k+b=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
则直线AB的函数解析式为:y=-x+2;
(2)如图1,连结PE,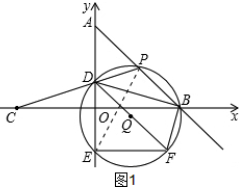
在△BDO和△CDO中,
$\left\{\begin{array}{l}{OC=OB}\\{∠DOB=∠DOC}\\{OD=OD}\end{array}\right.$,
∴△BDO≌△CDO,
∴∠BDO=∠CDO,
∵∠CDO=∠ADP,
∴∠BDE=∠ADP,
∵∠ADP是△DPE的一个外角,
∴∠ADP=∠DEP+∠DPE,
∵∠BDE是△ABD的一个外角,
∴∠BDE=∠ABD+∠OAB,
∵∠ADP=∠BDE,∠DEP=∠ABD,
∴∠DPE=∠OAB,
∵OA=OB=6,∠AOB=90°,
∴∠OAB=45°,
∴∠DPE=45°,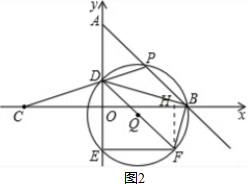
∴∠DFE=∠DPE=45°,
∵DF是⊙Q的直径,
∴∠DEF=90°,
∴∠DFE=45°;
(3)当BD:BF=2:1时,
①如图2,过点F作FH⊥OB于点H,
∵∠DBO+∠OBF=90°,∠OBF+∠BFH=90°,
∴∠DBO=∠BFH,
又∵∠DOB=∠BHF=90°,
∴△BOD∽△FHB,
∴$\frac{OB}{HF}$=$\frac{OD}{HB}$=$\frac{BD}{FB}$=2,
∴FH=1,OD=2BH,
∵∠FHO=∠EOH=∠OEF=90°,
∴四边形OEFH是矩形,
∴OE=FH=1,
∴EF=OH=2-$\frac{1}{2}$OD,
∵DE=EF,
∴1+OD=2-$\frac{1}{2}$OD,
解得:OD=$\frac{2}{3}$,
∴点D的坐标为(0,$\frac{2}{3}$),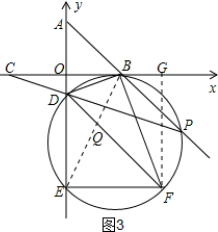
∴直线CD的解析式为y=$\frac{1}{3}$x+$\frac{2}{3}$,
$\left\{\begin{array}{l}{y=\frac{1}{3}x+\frac{2}{3}}\\{y=-x+2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
∴点P的坐标为(1,1);
当BD:BF=1:2时,
如图3,连结EB,同(2)可得:∠ADB=∠EDP,
∠ADB=∠DEB+∠DBE,∠EDP=∠DAP+∠DPA,
∵∠DEB=∠DPA,
∴∠DBE=∠DAP=45°,
∴△DEF是等腰直角三角形,过点F作FG⊥OB于点G,
同理可得:△BOD∽△FGB,
$\frac{OB}{GF}$=$\frac{OD}{GB}$=$\frac{BD}{FB}$=$\frac{1}{2}$,
∴FG=4,OD=$\frac{1}{2}$BG,
∵∠FGO=∠GOE=∠OEF=90°,
∴四边形OEFG是矩形,
∴OE=FG=4
∴EF=OG=2+2OD,
∵DE=EF,
∴4-OD=2+2OD,
解得,OD=$\frac{2}{3}$,
∴点D的坐标为(0,-$\frac{2}{3}$)
直线CD的解析式为:y=-$\frac{1}{3}$x-$\frac{2}{3}$,
∴点P的坐标为(4,-2),
综上所述,点P的坐标为(1,1)或(4,-2).
点评 此题主要考查了圆的综合,用到的知识点是一次函数、矩形的性质、圆的性质,关键是综合运用有关知识作出辅助线,列出方程组.


科目:初中数学 来源: 题型:解答题
型号 金额 | Ⅰ型设备 | Ⅱ型设备 | |||
| 投资金额x(万元) | x | 5 | x | 2 | 4 |
| 补贴金额y(万元) | y1=kx(k≠0) | 2 | y2=ax2+bx(a≠0) | 2.8 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(立方米) | 水费(元) |
| 3 | 28 | 56 |
| 4 | 20 | 35.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
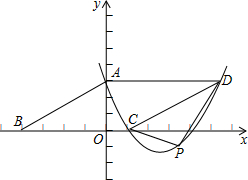 如图所示,在平面直角坐标系中,△ABC的顶点坐标分别为点A(0,3)、B(-4,0)、C(1,0),沿AC所在直线将△ABC翻折使点B落在点D处,抛物线y=ax2+bx+c经过A、C、D三点.
如图所示,在平面直角坐标系中,△ABC的顶点坐标分别为点A(0,3)、B(-4,0)、C(1,0),沿AC所在直线将△ABC翻折使点B落在点D处,抛物线y=ax2+bx+c经过A、C、D三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com