
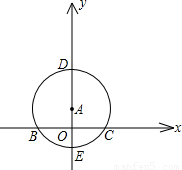
 x2-1交点坐标,横坐标x的范围就在两个交点之间.
x2-1交点坐标,横坐标x的范围就在两个交点之间.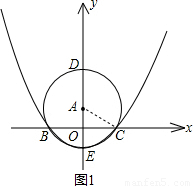
 DE=2
DE=2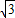
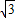 ,0),B(
,0),B(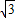 ,0)
,0)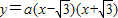 ,
,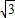 )(0+
)(0+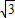 )
)
 (x-
(x- )(x+
)(x+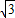 )=
)= x2-1(2分).
x2-1(2分).
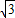 ,0),B(-
,0),B(-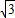 ,0)
,0)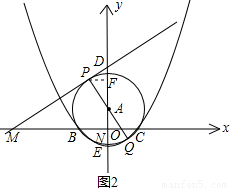

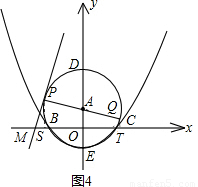
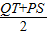
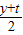

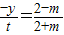 &&(1)
&&(1)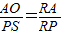
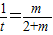 &&(2)
&&(2)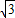
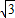 ,2)
,2)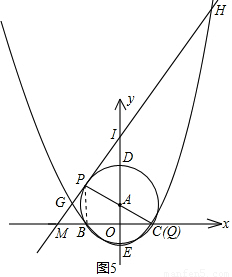 0°
0°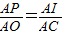
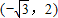 ,
,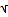 3 k+5.
3 k+5.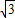 ,
,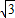 x+5(7分)
x+5(7分) x2-1交于G、H两点
x2-1交于G、H两点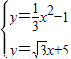
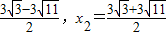
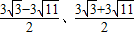
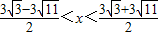 (9分)
(9分)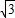 ,2)
,2)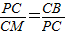
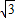 ,PC=4
,PC=4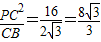
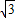 -m=
-m=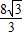
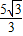 .
.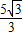 ,0).
,0).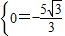 k+b2=-
k+b2=-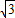 k+b.
k+b.
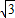 x+5(7分)
x+5(7分)

 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
 (1998•南京)已知:如图,点P在∠AOB的边OA上.
(1998•南京)已知:如图,点P在∠AOB的边OA上.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC于H、G,∠A=∠D,∠FGB+∠EHG=180°,问AB与CD有怎样的位置关系?为什么?
已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC于H、G,∠A=∠D,∠FGB+∠EHG=180°,问AB与CD有怎样的位置关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com