
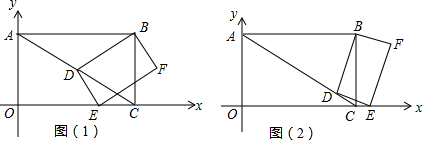
分析 (1)求出AB、BC的长即可解决问题;
(2)存在.连接BE,取BE的中点K,连接DK、KC.首先证明B、D、E、C四点共圆,可得∠DBC=∠DCE,∠EDC=∠EBC,由tan∠ACO=$\frac{AO}{OC}$=$\frac{\sqrt{3}}{3}$,推出∠ACO=30°,∠ACD=60°由△DEC是等腰三角形,观察图象可知,只有ED=EC,推出∠DBC=∠DCE=∠EDC=∠EBC=30°,推出∠DBC=∠BCD=60°,可得△DBC是等边三角形,推出DC=BC=2,由此即可解决问题;
(3)①由(2)可知,B、D、E、C四点共圆,推出∠DBC=∠DCE=30°,由此即可解决问题;
②作DH⊥AB于H.想办法用x表示BD、DE的长,构建二次函数即可解决问题;
解答 解:(1)∵四边形AOCB是矩形,
∴BC=OA=2,OC=AB=2$\sqrt{3}$,∠BCO=∠BAO=90°,
∴B(2$\sqrt{3}$,2).
故答案为(2$\sqrt{3}$,2).
(2)存在.理由如下:
连接BE,取BE的中点K,连接DK、KC.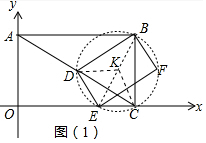
∵∠BDE=∠BCE=90°,
∴KD=KB=KE=KC,
∴B、D、E、C四点共圆,
∴∠DBE=∠DCE,∠EDC=∠EBC,
∵tan∠ACO=$\frac{AO}{OC}$=$\frac{\sqrt{3}}{3}$,
∴∠ACO=30°,∠ACB=60°
①如图1中,当E在线段CO上时,△DEC是等腰三角形,观察图象可知,只有ED=EC,
∴∠DBE=∠DCE=∠EDC=∠EBC=30°,
∴∠DBC=∠BCD=60°,
∴△DBC是等边三角形,
∴DC=BC=2,
在Rt△AOC中,∵∠ACO=30°,OA=2,
∴AC=2AO=4,
∴AD=AC-CD=4-2=2.
∴当AD=2时,△DEC是等腰三角形.
②如图2中,当E在OC的延长线上时,△DCE是等腰三角形,只有CD=CE,∠DBC=∠DEC=∠CDE=15°,
∴∠ABD=∠ADB=75°,
∴AB=AD=2$\sqrt{3}$,
综上所述,满足条件的AD的值为2或2$\sqrt{3}$.
(3)①由(2)可知,B、D、E、C四点共圆,
∴∠DBE=∠DCO=30°,
∴tan∠DBE=$\frac{DE}{DB}$,
∴$\frac{DE}{DB}$=$\frac{\sqrt{3}}{3}$.
②如图2中,作DH⊥AB于H.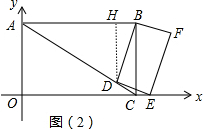
在Rt△ADH中,∵AD=x,∠DAH=∠ACO=30°,
∴DH=$\frac{1}{2}$AD=$\frac{1}{2}$x,AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=$\frac{\sqrt{3}}{2}$x,
∴BH=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x,
在Rt△BDH中,BD=$\sqrt{B{H}^{2}+D{H}^{2}}$=$\sqrt{(\frac{1}{2}x)^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2}x)^{2}}$,
∴DE=$\frac{\sqrt{3}}{3}$BD=$\frac{\sqrt{3}}{3}$•$\sqrt{(\frac{1}{2}x)^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2}x)^{2}}$,
∴矩形BDEF的面积为y=$\frac{\sqrt{3}}{3}$[$\sqrt{(\frac{1}{2}x)^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2}x)^{2}}$]2=$\frac{\sqrt{3}}{3}$(x2-6x+12),
即y=$\frac{\sqrt{3}}{3}$x2-2$\sqrt{3}$x+4$\sqrt{3}$,
∴y=$\frac{\sqrt{3}}{3}$(x-3)2+$\sqrt{3}$,
∵$\frac{\sqrt{3}}{3}$>0,
∴x=3时,y有最小值$\sqrt{3}$.
点评 本题考查相似形综合题、四点共圆、锐角三角函数、相似三角形的判定和性质、勾股定理、二次函数的性质等知识,解题的关键是学会添加辅助线,证明B、D、E、C四点共圆,学会构建二次函数解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 调查人数 | 视力不良 | 视力不良率(精确到0.01) | |
| 男生 | 1400 | 750 | 54% |
| 女生 | 1600 | m | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(元) | 200 | 240 | 270 | 300 |
| y(间) | 90 | 70 | 55 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$-1)0=1 | B. | (-3)2÷$\frac{9}{4}$=$\frac{1}{4}$ | C. | 5x2-6x2=-x2 | D. | (2m3)2÷(2m)2=m4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
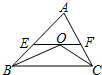 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )| A. | 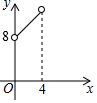 | B. | 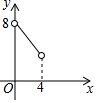 | C. | 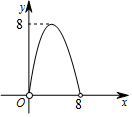 | D. | 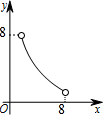 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
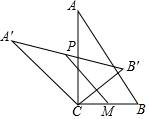 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
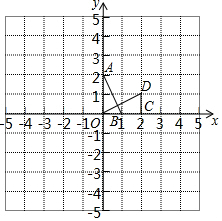 如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:△OCD绕C点顺时针旋转90°,并向左平移2个单位得到△AOB.
如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:△OCD绕C点顺时针旋转90°,并向左平移2个单位得到△AOB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com