
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,顶点为
,顶点为![]() .
.
(1)求这条抛物线的表达式和顶点![]() 的坐标;
的坐标;
(2)点![]() 关于抛物线对称轴的对应点为点
关于抛物线对称轴的对应点为点![]() ,联结
,联结![]() ,求
,求![]() 的正切值;
的正切值;
(3)将抛物线![]() 向上平移
向上平移![]() 个单位,使顶点
个单位,使顶点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,如果
处,如果![]() ,求
,求![]() 的值.
的值.
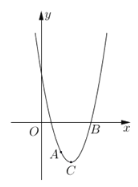
【答案】(1)![]() ,
,![]() ;(2)3;(3)
;(2)3;(3)![]()
【解析】
(1)根据待定系数法,即可求解;
(2)根据题意,画出图形,由OD=![]() ,OB=5,可得:∠OBD=∠ODB,即可求解;
,OB=5,可得:∠OBD=∠ODB,即可求解;
(3)根据题意:可得:BE=![]() ,BF=t,列出关于t的方程,即可求解.
,BF=t,列出关于t的方程,即可求解.
(1)∵抛物线![]() 经过点
经过点![]() 和点
和点![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴抛物线的表达式是:![]() ,
,
即:![]() ,
,
∴![]() ;
;
(2)∵抛物线的对称轴是:直线x=3,点![]() 关于抛物线对称轴的对应点为点
关于抛物线对称轴的对应点为点![]() ,
,
∴点D的坐标(4,-3),
∴OD=![]() ,
,
∵OB=5,
∴OB=OD,
∴∠OBD=∠ODB,
过点D作DE⊥x轴,则DE=3,BE=5-4=1,
∴tan∠ODB=tan∠OBD=![]() =3;
=3;
(3)∵抛物线![]() 向上平移
向上平移![]() 个单位,使顶点
个单位,使顶点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,
处,
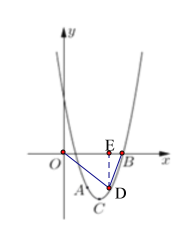
∴E(3,-4+t),F(5,t),
∴BE=![]() =
=![]() ,BF=t,
,BF=t,
∵![]() ,
,
∴![]() =t,解得:t=
=t,解得:t=![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知实数m,n满足(2m2+n2+1)(2m2+n2-1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81,
所以t=土9,因为2m2+n2>0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整休,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
(1)已知实数x、y,满足(2x2+2y2+3)(2x2+2y2-3)=27,求x2+y2的值.
(2)已知Rt△ACB的三边为a、b、c(c为斜边),其中a、b满足(a2+b2)(a2+b2-4)=5,求Rt△ACB外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
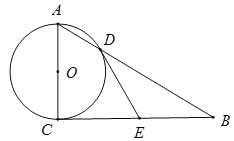
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系:_________;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0,
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根?
(2)当Rt△ABC的斜边a=![]() ,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合实践:
问题情境
数学活动课上,老师和同学们在正方形中利用旋转变换探究线段之间的关系探究过程如下所示:如图I,在正方形![]() 中,点
中,点![]() 为边
为边![]() 的中点.将
的中点.将![]() 以点
以点![]() 为旋转中心,顺时针方向旋转,当点
为旋转中心,顺时针方向旋转,当点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上时,连接
上时,连接![]() .
.

“兴趣小组”发现的结论是:![]() ;
;
“卓越小组”发现的结论是:![]() .
.
解决问题
(1)请你证明“兴趣小组”和“卓越小组”发现的结论;
拓展探究
证明完“兴趣小组”和“卓越小组”发现的结论后,“智慧小组”提出如下问题:如图2,连接![]() ,若正方形
,若正方形![]() 的边长为
的边长为![]() ,求出
,求出![]() 的长度.
的长度.
(2)请你帮助智慧小组写出线段![]() 的长度.(直接写出结论即可)
的长度.(直接写出结论即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级一班和二班各派出10名学生参加一分钟跳绳比赛,成绩如下表:
跳绳成绩(个) | 132 | 133 | 134 | 135 | 136 | 137 |
一班人数(人) | 1 | 0 | 1 | 5 | 2 | 1 |
二班人数(人) | 0 | 1 | 4 | 1 | 2 | 2 |
(1)两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表:
众数 | 中位数 | 平均数 | 方差 | |
一班 | a | 135 | 135 | c |
二班 | 134 | b | 135 | 1.8 |
表中数据a= ,b= ,c= ;
(2)请用所学的统计知识,从两个角度比较两个班跳绳比赛的成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
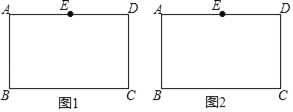
【题目】如图,在矩形ABCD中,点E为AD的中点,不用圆规、量角器等工具,只用无刻度的直尺作图.
(1)如图1,在BC上找点F,使点F是BC的中点;
(2)如图2,连接AC,在AC上取两点P,Q,使P,Q是AC的三等分点.
查看答案和解析>>
科目:初中数学 来源: 题型:
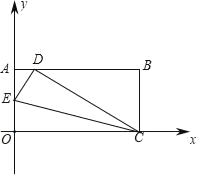
【题目】将一矩形纸片OABC放在直角坐标系中,O为原点C在x轴上,OA=5,OC=13,如图所示,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,则E点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com