
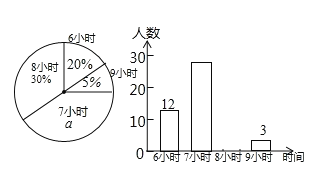
【题目】为了了解某校初中各年级学生每天的平均睡眠时间(单位:h,精确到1h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数a的值为 ,所抽查的学生人数为 .
(2)求出平均睡眠时间为8小时的人数,并补全频数直方图.
(3)求出这部分学生的平均睡眠时间的众数和平均数.
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
【答案】(1)45%,60;(2)见解析18;(3)7,7.2;(4)780
【解析】
(1)根据睡眠时间为6小时、7小时、8小时、9小时的百分比之和为1可得a的值,用睡眠时间为6小时的人数除以所占的比例即可得到抽查的学生人数;
(2)用抽查的学生人数乘以睡眠时间为8小时所占的比例即可得到结果;
(3)根据众数,平均数的定义即可得到结论;
(4)用学生总数乘以抽样中睡眠不足(少于8小时)的学生数所占的比例列式计算即可.
(1)a=1﹣20%﹣30%﹣5%=45%;
所抽查的学生人数为:3÷5%=60(人).
故答案为:45%,60;
(2)平均睡眠时间为8小时的人数为:60×30%=18(人);
(3)这部分学生的平均睡眠时间的众数是7人,
平均数![]() 7.2(小时);
7.2(小时);
(4)1200名睡眠不足(少于8小时)的学生数![]() 1200=780(人).
1200=780(人).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣3,﹣2,﹣1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
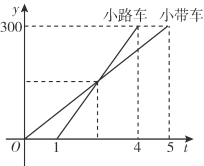
【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=![]() 或t=
或t=![]() .其中正确的结论有( )
.其中正确的结论有( )
A. ①②③④B. ①②④
C. ①②D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以每件50元的价格购进800件![]() 恤,第一个月以单价80元销售,售出了200件.第二个月如果单价不变,预计仍可售出200件,该商店为增加销售量决定降价销售,根据市场调查,单价每降低1元,可多销售出10件,但最低单价应不低于50元,第二个月结束后,该商店对剩余的T恤一次性清仓,清仓时单价为40元.设第二个月单价降低
恤,第一个月以单价80元销售,售出了200件.第二个月如果单价不变,预计仍可售出200件,该商店为增加销售量决定降价销售,根据市场调查,单价每降低1元,可多销售出10件,但最低单价应不低于50元,第二个月结束后,该商店对剩余的T恤一次性清仓,清仓时单价为40元.设第二个月单价降低![]() 元,
元,
(1)填表(用含![]() 的代数式完成表格中的①②③处)
的代数式完成表格中的①②③处)
时间 | 第一个月 | 第二个月 | 清仓 |
单价(元) | 80 | _______ | 40 |
销售量(件) | 200 | _______ | _______ |
(2)如果该商店希望通过销售这800件![]() 恤获利9000元,那么第二个月单价降低多少元?
恤获利9000元,那么第二个月单价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在平行四边形![]() 中,点
中,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
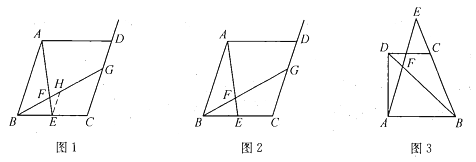
(1)尝试探究
在图1中,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则
,则![]() 和
和![]() 的数量关系是______,
的数量关系是______,![]() 和
和![]() 的数量关系是______,
的数量关系是______,![]() 的值是______;
的值是______;
(2)类比延伸
如图2,在原题的条件下,当![]() 时,参照问题(1)的研究结论,请你猜想
时,参照问题(1)的研究结论,请你猜想![]() 的值(用含
的值(用含![]() 的代数式表示),并证明你的猜想;
的代数式表示),并证明你的猜想;
(3)拓展迁移
如图3,梯形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 和
和![]() 相交于点
相交于点![]() ,当
,当![]() ,
,![]() 时,请你求出
时,请你求出![]() 的值(用含
的值(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称次抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点的横坐标为﹣1,求“带线”L的表达式;
(2)如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系,求m,n的值;
(3)设(2)中的“带线”L与它的“路线”l在y轴上的交点为A.已知点P为“带线”L上的点,当以点P为圆心的圆与“路线”l相切于点A时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过![]() ,
,![]() 及原点
及原点![]() ,顶点为
,顶点为![]() .
.
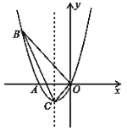
(1)求抛物线的函数解析式;
(2)设点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,且以
在抛物线的对称轴上,且以![]() 、
、![]() 、
、![]() ,
,![]() 为顶点,
为顶点,![]() 为边的四边形是平行四边形,求点
为边的四边形是平行四边形,求点![]() 的坐标;
的坐标;
(3)![]() 是抛物线上第一象限内的动点,过点
是抛物线上第一象限内的动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .是否存在这样的点
.是否存在这样的点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别交射线
分别交射线![]() 、射线
、射线![]() 于点
于点![]() 、
、![]() .
.
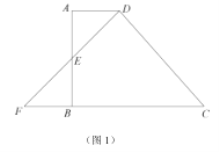
(1)当点![]() 为边
为边![]() 的中点时(如图1),求
的中点时(如图1),求![]() 的长:
的长:
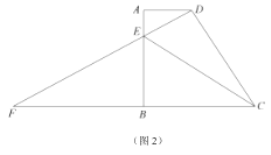
(2)当点![]() 在边
在边![]() 上时(如图2),联结
上时(如图2),联结![]() ,试问:
,试问:![]() 的大小是否确定?若确定,请求出
的大小是否确定?若确定,请求出![]() 的正切值;若不确定,则设
的正切值;若不确定,则设![]() ,
,![]() 的正切值为
的正切值为![]() ,请求出
,请求出![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)当![]() 的面积为3时,求
的面积为3时,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com