
分析 (1)设甲种奖品购买了x件,乙种奖品购买了(20-x)件,利用购买甲、乙两种奖品共花费了650元列方程40x+30(20-x)=650,然后解方程求出x,再计算20-x即可;
(2)设甲种奖品购买了x件,乙种奖品购买了(20-x)件,利用购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元列不等式组$\left\{\begin{array}{l}{20-x≤2x}\\{40x+30(20-x)≤680}\end{array}\right.$,然后解不等式组后确定x的整数值即可得到该公司的购买方案.
解答 解:(1)设甲种奖品购买了x件,乙种奖品购买了(20-x)件,
根据题意得40x+30(20-x)=650,
解得x=5,
则20-x=15,
答:甲种奖品购买了5件,乙种奖品购买了15件;
(2)设甲种奖品购买了x件,乙种奖品购买了(20-x)件,
根据题意得$\left\{\begin{array}{l}{20-x≤2x}\\{40x+30(20-x)≤680}\end{array}\right.$,解得$\frac{20}{3}$≤x≤8,
∵x为整数,
∴x=7或x=8,
当x=7时,20-x=13;当x=8时,20-x=12;
答:该公司有2种不同的购买方案:甲种奖品购买了:7件,乙种奖品购买了13件或甲种奖品购买了8件,乙种奖品购买了12件.
点评 本题考查了一元一次不等式组的应用:对具有多种不等关系的问题,考虑列一元一次不等式组,并求解;一元一次不等式组的应用主要是列一元一次不等式组解应用题,


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
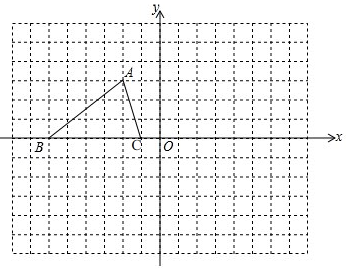 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
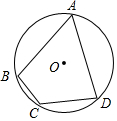 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
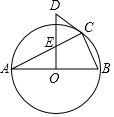 如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
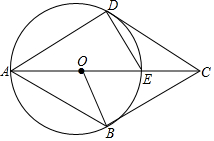 已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D.B点在⊙O上,连接OB.
已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D.B点在⊙O上,连接OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com