
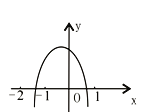
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③a<-1;④b2+8a>4ac,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题解析:由图知:抛物线的开口向下,则a<0;抛物线的对称轴x=-![]() >-1,且c>0;
>-1,且c>0;
①由图可得:当x=-2时,y<0,即4a-2b+c<0,故①正确;
②已知x=-![]() >-1,且a<0,所以2a-b<0,故②正确;
>-1,且a<0,所以2a-b<0,故②正确;
③已知抛物线经过(-1,2),即a-b+c=2(1),由图知:当x=1时,y<0,即a+b+c<0(2),
由①知:4a-2b+c<0(3);联立(1)(2),得:a+c<1;联立(1)(3)得:2a-c<-4;
故3a<-3,即a<-1;所以③正确;
④由于抛物线的对称轴大于-1,所以抛物线的顶点纵坐标应该大于2,即:
![]() >2,由于a<0,所以4ac-b2<8a,即b2+8a>4ac,故④正确;
>2,由于a<0,所以4ac-b2<8a,即b2+8a>4ac,故④正确;
因此正确的结论是①②③④.
故选D.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
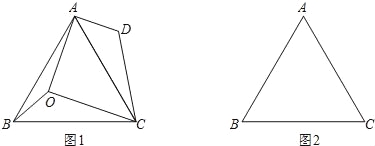
【题目】已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是 ;
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= ![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( ) 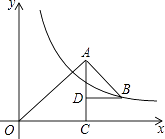
A.36
B.12
C.6
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道|5|=|5-0|,它在数轴上的意义是表示5的点与原点(即表示0的点)之间的距离.又如式子|6-3|,它在数轴上的意义是表示6的点与表示3的点之间的距离.则|x-100|+|x-50|+|x+100|的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一副三角尺拼成的图案
(1)则∠EBC的度数为 _________ 度;
(2)将图1中的三角尺ABC绕点B旋转到AB⊥BD时,作∠DBC的角平分线BF,直接写出∠EBF的度数是 _________ 度;
(3)将图1中的三角尺ABC绕点B旋转α度(0°<α<90°)能否使∠ABE=2∠DBC?若能,则求出∠EBC的度数;若不能,说明理由.(图2、图3供参考)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com