
【题目】设[a]表示不超过a的最大整数,例如:[2.3]=2,[﹣4 ![]() ]=﹣5,[5]=5.
]=﹣5,[5]=5.
(1)求[2 ![]() ]+[﹣3.6]﹣[﹣7]的值;
]+[﹣3.6]﹣[﹣7]的值;
(2)令[a]=a﹣[a],求{2 ![]() }﹣[﹣2.4]+{﹣6
}﹣[﹣2.4]+{﹣6 ![]() }.
}.
【答案】
(1)解:[2 ![]() ]+[﹣3.6]﹣[﹣7],
]+[﹣3.6]﹣[﹣7],
=2+(﹣4)﹣(﹣7),
=2﹣4+7,
=5;
(2)解:{2 ![]() }﹣[﹣2.4]+{﹣6
}﹣[﹣2.4]+{﹣6 ![]() },
},
=2 ![]() ﹣[2
﹣[2 ![]() ]+2.4+[﹣2.4]+(﹣6
]+2.4+[﹣2.4]+(﹣6 ![]() )﹣[﹣6
)﹣[﹣6 ![]() ],
],
= ![]() ﹣2+2.4﹣3﹣
﹣2+2.4﹣3﹣ ![]() +7,
+7,
=4.4﹣ ![]() ,
,
=4.4﹣3.5,
=0.9
【解析】(1)根据新定义得:[2 ![]() ]=2,[﹣3.6]=﹣4,[﹣7]=﹣7,再代入计算即可;(2)根据新定义得:{2
]=2,[﹣3.6]=﹣4,[﹣7]=﹣7,再代入计算即可;(2)根据新定义得:{2 ![]() }=2
}=2 ![]() ﹣[2
﹣[2 ![]() ]=2
]=2 ![]() ﹣2,[﹣2.4]=﹣2.4﹣[﹣2.4]=﹣2.4﹣(﹣3)=﹣2.4+3,{﹣6
﹣2,[﹣2.4]=﹣2.4﹣[﹣2.4]=﹣2.4﹣(﹣3)=﹣2.4+3,{﹣6 ![]() }=﹣6
}=﹣6 ![]() ﹣[﹣6
﹣[﹣6 ![]() ]=﹣6
]=﹣6 ![]() +7,再代入原式进行计算.
+7,再代入原式进行计算.
【考点精析】认真审题,首先需要了解有理数的加减混合运算(混合运算法则:先乘方,后乘除,最后加减),还要掌握有理数大小比较(有理数比大小:1、正数的绝对值越大,这个数越大2、正数永远比0大,负数永远比0小3、正数大于一切负数4、两个负数比大小,绝对值大的反而小5、数轴上的两个数,右边的数总比左边的数大6、大数-小数 > 0,小数-大数 < 0)的相关知识才是答题的关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某公园的成人票价是15元,儿童买半票,甲旅行团有x(名)成年人和y(名)儿童,乙旅行团的成人数是甲旅行团的2倍,儿童数比甲旅行团的2倍少8人.这两个旅行团的门票费用总和各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数有( ) ①若干个不为0的有理数相乘,积的符号由负因数的个数决定;②两个四次多项式的和一定是四次多项式;③若a大于b,则a的倒数小于b的倒数;④若xyz<0,则 ![]() 的值为0或﹣4.
的值为0或﹣4.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点对应的有理数分别为20和30,点P和点Q分别同时从点A和点O出发,以每秒2个单位长度,每秒4个单位长度的速度向数轴正方向运动,设运动时间为t秒. ![]()
(1)当t=2时,则P、Q两点对应的有理数分别是;PQ=;
(2)点C是数轴上点B左侧一点,其对应的数是x,且CB=2CA,求x的值;
(3)在点P和点Q出发的同时,点R以每秒8个单位长度的速度从点B出发,开始向左运动,遇到点Q后立即返回向右运动,遇到点P后立即返回向左运动,与点Q相遇后再立即返回,如此往返,直到P、Q两点相遇时,点R停止运动,求点R运动的路程一共是多少个单位长度?点R停止的位置所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式错误的是( )
A.(2mn)2=4m2n2
B.(﹣2mn)2=4m2n2
C.(2m2n2)3=8m6n6
D.(﹣2m2n2)3=﹣8m5n5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(6,0),在B在y轴的正半轴上,且S△AOB=24.
(1)求点B坐标;
(2)若点P从B出发沿y轴负半轴运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB , 在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由.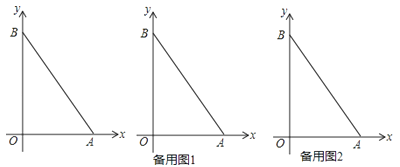
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com